A proton of mass m and charge q enters a magnetic field B with a velocity v at an angle θ with the direction of B.The radius of curvature of the resulting path is
mvqB
mvsinθqB
mvqBsinθ
mvcosθqB
The correct Answer is:B
To find the radius of curvature of a proton moving in a magnetic field at an angle, we can follow these steps:
1. Identify the Given Parameters:
- Mass of the proton: m
- Charge of the proton: q
- Velocity of the proton: v
- Magnetic field strength: B
- Angle between the velocity and the magnetic field: θ
2. Break Down the Velocity into Components:
- The velocity v can be resolved into two components:
- Perpendicular to the magnetic field: v⊥=vsinθ
- Parallel to the magnetic field: v∥=vcosθ
3. Determine the Magnetic Force:
- The magnetic force acting on the proton is given by:
F=q(v⊥×B)=q(vsinθ)B
- Since v⊥ is perpendicular to the magnetic field, we can simplify this to:
F=qvsinθB
4. Relate the Magnetic Force to Centripetal Force:
- For a charged particle moving in a circular path, the magnetic force provides the centripetal force required for circular motion:
F=mv2⊥r
- Substituting v⊥=vsinθ:
F=m(vsinθ)2r
5. Set the Forces Equal:
- Equating the magnetic force and the centripetal force:
qvsinθB=m(vsinθ)2r
6. Rearranging for Radius r:
- Rearranging the equation to solve for r:
r=m(vsinθ)qB
- This can be simplified to:
r=mvqBsinθ
Final Result:
The radius of curvature r of the proton's path in the magnetic field is given by:
r=mvqBsinθ
- Mass of the proton: m
- Charge of the proton: q
- Velocity of the proton: v
- Magnetic field strength: B
- Angle between the velocity and the magnetic field: θ
- The velocity v can be resolved into two components:
- Perpendicular to the magnetic field: v⊥=vsinθ
- Parallel to the magnetic field: v∥=vcosθ
- The magnetic force acting on the proton is given by:
F=q(v⊥×B)=q(vsinθ)B
- Since v⊥ is perpendicular to the magnetic field, we can simplify this to:
F=qvsinθB
- For a charged particle moving in a circular path, the magnetic force provides the centripetal force required for circular motion:
F=mv2⊥r
- Substituting v⊥=vsinθ:
F=m(vsinθ)2r
- Equating the magnetic force and the centripetal force:
qvsinθB=m(vsinθ)2r
- Rearranging the equation to solve for r:
r=m(vsinθ)qB
- This can be simplified to:
r=mvqBsinθ
The radius of curvature r of the proton's path in the magnetic field is given by:
r=mvqBsinθ
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-1
15 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-2
26 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-1 PART-1
83 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
A charged particle of mass m & charge q enters a zone of uniform magnetic field B with a velocity v making an angle θ with the boundary of the zone, having width d, when the particle penetrates half-way into the zone, the change in energy of the particel is
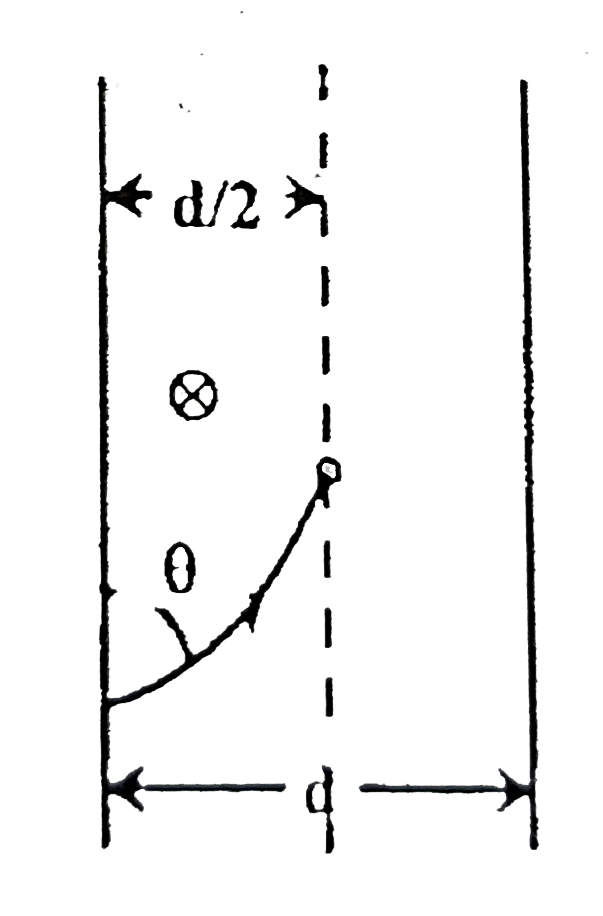
View SolutionA charged particle enters in a magnetic field B with its initial velocity making an angle of 45° with B. The path of the particle will be
View SolutionA particle of mass m and charge +q enters a region of magnetic field with a velocity v, as shown in Fig. 1.93.
a. Find the angle subtended by the circular arc described by it in the magnetic field.
b. How long does the particle stay inside the magnetic field?
c. If the particle enters at E, what is the intercept EF?

View SolutionA proton of mass m and charge q enters a region of uniform magnetic field of a magnitude B with a velocity v directed perpendicular to the magnetic field. It moves in a circular path and leaves the magnetic field after completing a quarter of a circle. The time spent by the proton inside the magnetic field is proportional to:
View SolutionA proton and anα-particles enters in a uniform magnetic field with same velocity, then ratio of the radii of path describe by them
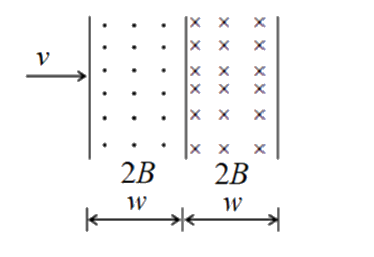
View SolutionThe figure shows two regions of uniform magnetic field of strengths 2B and 2B. A charged particle of mass m and charge q enters the region of the magnetic field with a velocity υ=qBwm, where w is the width of each region of the magnetic field. The time taken by the particle to come out of the region of the magnetic field is
View SolutionA charged particle enters a unifrom magnetic field with velocity vector at an angle of 45∘ with the magnetic field . The pitch of the helical path followed by the particles is ρ . The radius of the helix will be
View SolutionThere exist uniform magnetic field →B=−B0ˆk in region of space with 0<x<d and 2d<x<3d as shown in the figure. A positive charged particle of mass m and charge q is projected with velocity →v=vˆi as shown in the figure. If radius of curvature of path of the charged particle in magnetic field isR(2d<R<3d) then time elapse by charged particle in magnetic field regions is

View SolutionA charge q enters into a magnetic field (B) perpendicularly with velocity V. The time rate of work done by the magnetic force on the charge is
View SolutionA charge having q/m equal to 108 c/kg and with velocity 3×105 m/s enters into a uniform magnetic field B = 0.3 tesla at an angle 30∘ with direction of field. Then radius of curvature will be:
View Solution
