A coil of 50 turns and 20cm diameter is made with a wire of 0.2mm diameter and resistivity 2×10−6Ωcm.The coil is connected to a source of EMF20V and negligible internal resistance.
Find the current through the coil.
The correct Answer is:A, B, C, D
To find the current through the coil, we will follow these steps:
Step 1: Gather the given data
- Number of turns (N) = 50
- Diameter of the coil (d_c) = 20 cm = 0.2 m
- Diameter of the wire (d_w) = 0.2 mm = 0.2 x 10^(-3) m
- Resistivity (ρ) = 2 x 10^(-6) Ω cm = 2 x 10^(-8) Ω m
- EMF (V) = 20 V
Step 2: Convert the diameter of the coil to radius
- Radius of the coil (r_c) = d_c / 2 = 0.2 m / 2 = 0.1 m
Step 3: Convert the diameter of the wire to radius
- Radius of the wire (r_w) = d_w / 2 = (0.2 x 10^(-3) m) / 2 = 0.1 x 10^(-3) m = 1 x 10^(-4) m
Step 4: Calculate the length of the wire (L)
- The length of the wire can be calculated using the formula for the circumference of a circle multiplied by the number of turns:
L=N×(2πrc)=50×(2π×0.1)=50×0.2π=10π m
Step 5: Calculate the cross-sectional area of the wire (A)
- The cross-sectional area of the wire is given by:
A=πr2w=π(1×10−4)2=π×10−8 m2
Step 6: Calculate the resistance (R) of the wire
- The resistance can be calculated using the formula:
R=ρLA
Substituting the values:
R=(2×10−8)×(10π)π×10−8=2×10−8×10ππ×10−8=20 ohms
Step 7: Calculate the current (I) using Ohm's Law
- According to Ohm's Law:
I=VR
Substituting the values:
I=20 V20 ohms=1 A
Final Answer
The current through the coil is 1 A.
---
- Number of turns (N) = 50
- Diameter of the coil (d_c) = 20 cm = 0.2 m
- Diameter of the wire (d_w) = 0.2 mm = 0.2 x 10^(-3) m
- Resistivity (ρ) = 2 x 10^(-6) Ω cm = 2 x 10^(-8) Ω m
- EMF (V) = 20 V
- Radius of the coil (r_c) = d_c / 2 = 0.2 m / 2 = 0.1 m
- Radius of the wire (r_w) = d_w / 2 = (0.2 x 10^(-3) m) / 2 = 0.1 x 10^(-3) m = 1 x 10^(-4) m
- The length of the wire can be calculated using the formula for the circumference of a circle multiplied by the number of turns:
L=N×(2πrc)=50×(2π×0.1)=50×0.2π=10π m
- The cross-sectional area of the wire is given by:
A=πr2w=π(1×10−4)2=π×10−8 m2
- The resistance can be calculated using the formula:
R=ρLA
Substituting the values:
R=(2×10−8)×(10π)π×10−8=2×10−8×10ππ×10−8=20 ohms
- According to Ohm's Law:
I=VR
Substituting the values:
I=20 V20 ohms=1 A
The current through the coil is 1 A.
Topper's Solved these Questions
- ELECTRODYNAMICSBook:RESONANCE ENGLISHChapter:ELECTRODYNAMICSExercise:Exercise-1 PART-2
Explore 54 Videos
- ELECTRODYNAMICSBook:RESONANCE ENGLISHChapter:ELECTRODYNAMICSExercise:Exercise-2 PART-1
Explore 15 Videos
- ELECTRODYNAMICSBook:RESONANCE ENGLISHChapter:ELECTRODYNAMICSExercise:PROBLEM
Explore 12 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
Similar Questions
A coil of self inductance 2.5 H and resistance 20Ω is connected to a battery of emf 120 V having internal resistance of 5Ω. Find :
The current in the circuit in steady state.
View SolutionA coil of self inductance 2.5 H and resistance 20Ω is connected to a battery of emf 120 V having internal resistance of 5Ω. Find :
The time constant of the circuit
View Solution
Knowledge Check
A potentiometer wire of length 100 cm has a resistance of 100Ω it is connected in series with a resistance and a battery of emf 2 V and of negligible internal resistance. A source of emf 10 mV is balanced against a length of 40 cm of the potentiometer wire. what is the value of the external resistance?
A790ΩB890ΩC990ΩD1090Ω
A coil having self-inductance of 0.7 H and resistance of 165Ω is connected to a.c. source of 275 V, 50 Hz. Calculate :
(i) Reactance of the coil
(ii) Impedance of the coil
(iii) Current flowing through the coil.
View SolutionTwo coils of self inductance L1 and L2 are connected in parallel and then connected to a cell of emf ε and internal resistance - R. Find the steady state current in the coils.
View SolutionA coil having self-inductance of 0.7 H and resistance of 165Ω is connected to an a.c. source of 275 V, 50 Hz. If π=227 Calculate :
Current flowing through the coil.
View SolutionAB is a potentiometer wire of length 100 cm and its resistance is 10Ω. It is connected in series with a resistance R = 40 Ω and a battery of emf 2 V and negligible internal resistance. If a source of unknown emf E is balanced by 40 cm length of the potentiometer wire, the value of E is
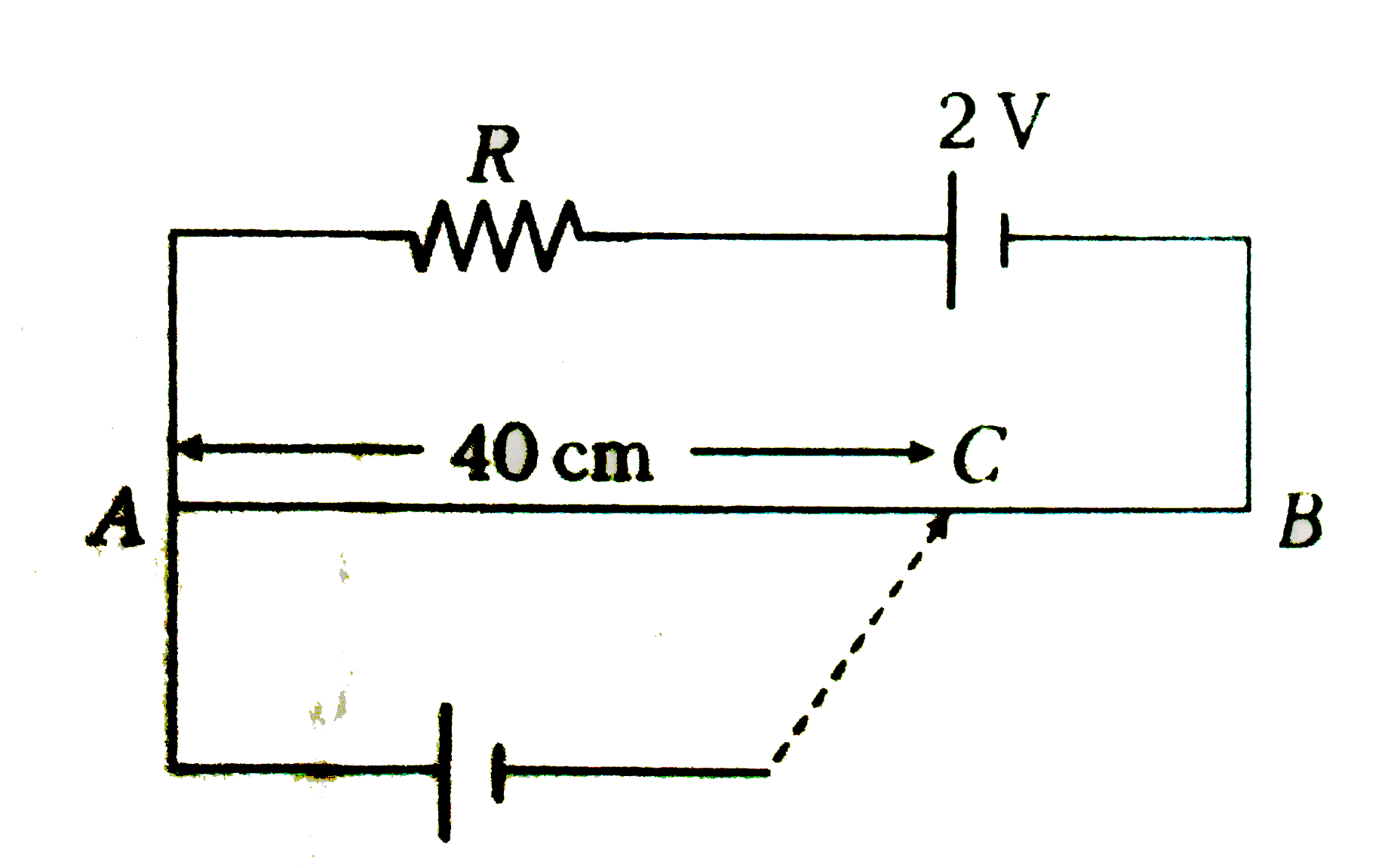
View SolutionTwo tangent galvanometers A and B have coils of radii 8cm and 16cm respectively and resistance 8ohm each. They are connected in parallel to a cell of emf 4V and negligible internal resistance. The deflections produced are 30∘ and 60∘ respectivley. A has 2 turns. What is the number of turns in B?
View SolutionA Capacitor and a coil in series are connected to a 6volt ac source. By varying the frequency of the source, maximum current of 600mA is observed. If the same coil is now connected toa cell of emf 6volt dc and internal resistance of 2ohm, the current h through it will be
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View Solution