A medium has nv=1.56,nr=1.44. Then its dispersive power is:
3/50
6/25
0.03
none of these
The correct Answer is:D
To find the dispersive power of a medium with given refractive indices for violet and red light, we can follow these steps:
1. Identify the Refractive Indices:
- Given:
- Refractive index for violet light, nv=1.56
- Refractive index for red light, nr=1.44
2. Calculate the Mean Refractive Index:
- The mean refractive index nm can be calculated as:
nm=nv+nr2=1.56+1.442=3.002=1.50
3. Calculate the Mean Deviation:
- The mean deviation Δm is given by:
Δm=nm−1=1.50−1=0.50
4. Calculate the Angular Dispersion:
- The angular dispersion Δθ can be calculated using the formula:
Δθ=(nv−nr)⋅A
- Where A is the angle of the prism. Thus:
Δθ=(1.56−1.44)⋅A=0.12⋅A
5. Calculate the Dispersive Power:
- The dispersive power ω is given by the ratio of angular dispersion to mean deviation:
ω=ΔθΔm
- Substituting the values we calculated:
ω=0.12⋅A0.50=0.120.50⋅A=1250⋅A=625⋅A
- Since A cancels out, the dispersive power is:
ω=625
Final Answer:
The dispersive power of the medium is 625.
---
- Given:
- Refractive index for violet light, nv=1.56
- Refractive index for red light, nr=1.44
- The mean refractive index nm can be calculated as:
nm=nv+nr2=1.56+1.442=3.002=1.50
- The mean deviation Δm is given by:
Δm=nm−1=1.50−1=0.50
- The angular dispersion Δθ can be calculated using the formula:
Δθ=(nv−nr)⋅A
- Where A is the angle of the prism. Thus:
Δθ=(1.56−1.44)⋅A=0.12⋅A
- The dispersive power ω is given by the ratio of angular dispersion to mean deviation:
ω=ΔθΔm
- Substituting the values we calculated:
ω=0.12⋅A0.50=0.120.50⋅A=1250⋅A=625⋅A
- Since A cancels out, the dispersive power is:
ω=625
The dispersive power of the medium is 625.
Topper's Solved these Questions
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-2
62 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-3
80 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Problem
33 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
Similar Questions
For a material medium, the values of refractive index for violet and colours are given as nv=1.56andnr=1.44. The dispersive power of a prism made out of this material is
View SolutionLight of wavelenght 4000A is incident at small angle on a prim of apex angle 4∘ . The prism has nv=1.5 and nr=1.48 . The angle of dispersion produced by the prism in this light is:
View SolutionWhen a ray of sun light passes through the prism, each colour of light has its own speed in the glass. The seven colours come out of the prism with different angles of deviation. Red deviates least and blue deviates maximum. Thus a prism can disperse a white light into seven colours which is called colour spectrum.

For a thin prism, the angle of deviation is given as δ=(n−1)A. The angle of dispersion is given as ϕ=δv−δr. The dispersive power of a prism is ω=ϕδmean=ϕδy
Using the above ideas, give answer the following questions.
A prism has R.I. for violet and red nv=1.523,nr=1.5145. If the angle of prism is A=2∘ the dispersive power of the prism is :
View SolutionDerive an expression for refraction at a single (convex) spherical surface, i.e., a relation between u, v, R, n1 (rarer medium) and n2 (denser medium), where the terms have their usual meaning.
View SolutionShow that the axial chromatic aberration. (fr−fv) for a convex lens is equal to the product of its mean focal length (f) and dispersive power (ω) of its materialie. Prove :
fr−fv=ωf
View SolutionA certain material has refractive indices 1.56, 1.60 and 1.68 for red, yellow and violet light respectively. (a) Calculate the dispersive power. (b) Find the angular dispersion produced by a thin prism of angle 6° made of this material.
View SolutionCalculate dispersive power of a transparent material given :
nv=1.56,nr=1.54,ny=1.55
View SolutionDefine dispersive power (for light) of a medium.
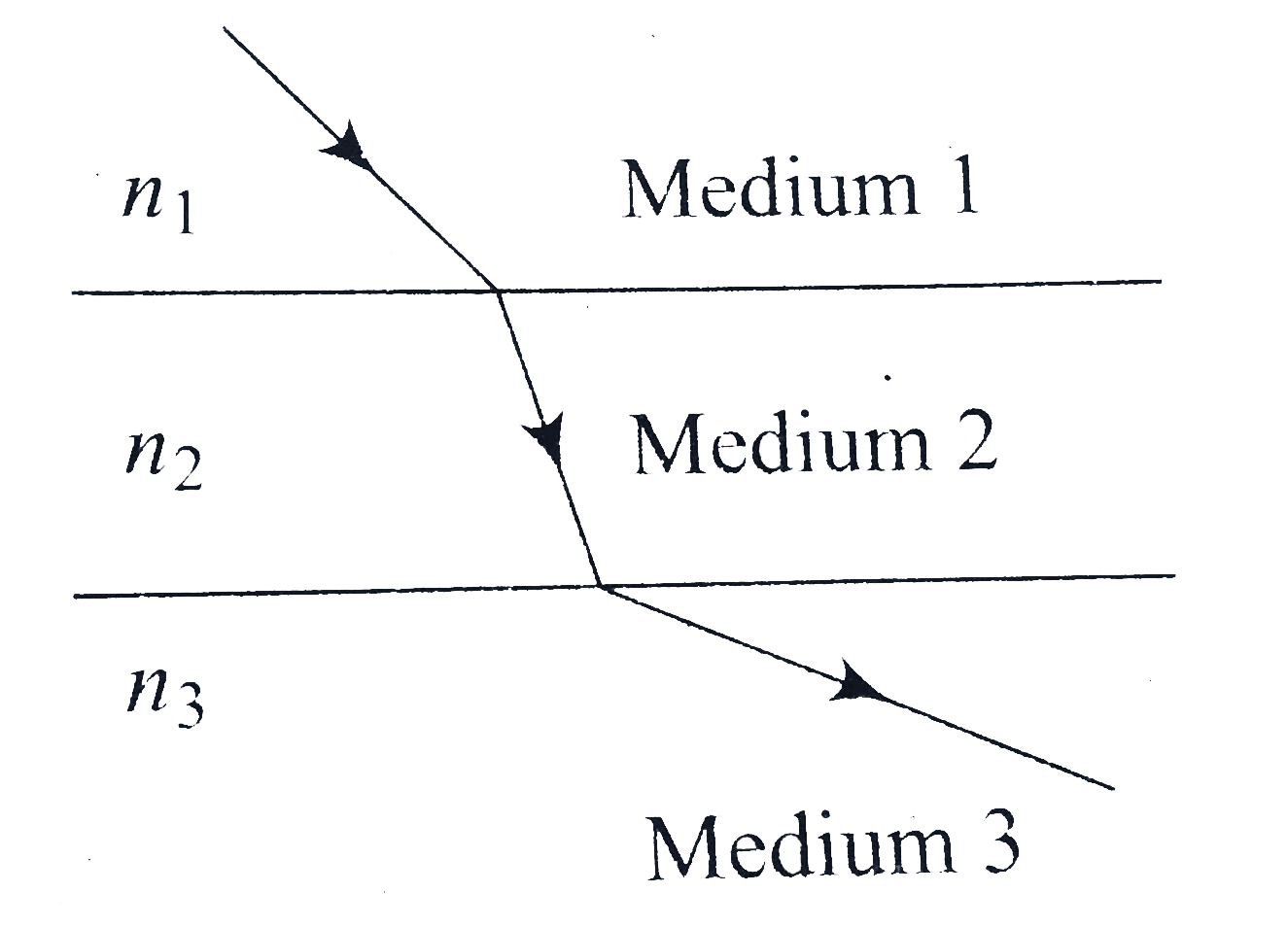
View SolutionA beam of light passes from medium 1 to medium 2 to medium 3 as shown figure. What may be concluded about the three indices of refraction, n1,n2,andn3 ?
View SolutionIf ^nPr=nPr+1andnCr=nCr−1, then the value of n+r is.
View Solution
