A wave moving with constant speed on a uniform string passes the point x=0 with amplitude A0, angular frequency ω0 and average rate of energy transfer P0. As the wave travels down the string it gradually loses energy and at the point x=l, the average rate of energy transfer becomesP0/2. At the point x=l. Angular frequency and amplitude are respectively:
ω0 and A0/√2
ω0/√2 and A0
less than ω0 and A0
ω0/√2 and A0/√2
The correct Answer is:A
To solve the problem step by step, we will analyze the energy transfer in the wave on the string and how it relates to amplitude and angular frequency.
Step 1: Understand the initial conditions
The wave at point x=0 has:
- Amplitude: A0
- Angular frequency: ω0
- Average rate of energy transfer: P0
Step 2: Write the expression for energy transfer
The average power (rate of energy transfer) for a wave on a string can be expressed as:
P=12μω2A2v
where:
- μ = mass per unit length of the string
- ω = angular frequency
- A = amplitude
- v = wave speed
Step 3: Write the initial power equation
At x=0:
P0=12μω20A20v
Step 4: Write the power equation at x=l
At x=l, the power is given as P02:
P02=12μω2A2v
Step 5: Relate the two power equations
From the two equations, we can relate the powers:
P0P02=12μω20A20v12μω2A2v
This simplifies to:
2=ω20A20ω2A2
Step 6: Isolate the variables
Rearranging gives:
ω2A2=A202ω20
Step 7: Find the amplitude at x=l
We can express the amplitude A at x=l:
A2=A202
Taking the square root:
A=A0√2
Step 8: Determine the angular frequency
Since the angular frequency depends on the source and is not affected by the energy loss in the wave, we have:
ω=ω0
Final Answer
At the point x=l:
- Amplitude A=A0√2
- Angular frequency ω=ω0
Summary of Results
- Amplitude at x=l: A=A0√2
- Angular frequency at x=l: ω=ω0
The wave at point x=0 has:
- Amplitude: A0
- Angular frequency: ω0
- Average rate of energy transfer: P0
The average power (rate of energy transfer) for a wave on a string can be expressed as:
P=12μω2A2v
where:
- μ = mass per unit length of the string
- ω = angular frequency
- A = amplitude
- v = wave speed
At x=0:
P0=12μω20A20v
At x=l, the power is given as P02:
P02=12μω2A2v
From the two equations, we can relate the powers:
P0P02=12μω20A20v12μω2A2v
This simplifies to:
2=ω20A20ω2A2
Rearranging gives:
ω2A2=A202ω20
We can express the amplitude A at x=l:
A2=A202
Taking the square root:
A=A0√2
Since the angular frequency depends on the source and is not affected by the energy loss in the wave, we have:
ω=ω0
At the point x=l:
- Amplitude A=A0√2
- Angular frequency ω=ω0
- Amplitude at x=l: A=A0√2
- Angular frequency at x=l: ω=ω0
Topper's Solved these Questions
- WAVE ON STRING Book:RESONANCE ENGLISHChapter:WAVE ON STRING Exercise:Exercise- 2 PART I
Explore 21 Videos
- WAVE ON STRING Book:RESONANCE ENGLISHChapter:WAVE ON STRING Exercise:Exercise- 2 PART II
Explore 19 Videos
- WAVE ON STRING Book:RESONANCE ENGLISHChapter:WAVE ON STRING Exercise:Exercise- 1 PART I
Explore 23 Videos
- TRAVELLING WAVESBook:RESONANCE ENGLISHChapter:TRAVELLING WAVESExercise:Exercise- 3 PART I
Explore 19 Videos
- WAVE OPTICSBook:RESONANCE ENGLISHChapter:WAVE OPTICSExercise:Advanced Level Problems
Explore 8 Videos
Similar Questions
Graph shows three waves that are separately sent along a string that is stretched under a certain tension along x-axis. If ω1,ω2andω3 are their angular frequencies, respectively, then:

View SolutionGraph shows three waves that are separately sent along a string that is stretched under a certain tension along x-axis. If ω1,ω2andω3 are their angular frequencies, respectively, then:

View SolutionA particle stars SHM at time t=0. Its amplitude is A and angular frequency is ω. At time t=0 its kinetic energy is E4. Assuming potential energy to be zero and the particle can be written as (E=total mechanical energy of oscillation).
View SolutionWhich of the following options is representing average energy per unit volume of a travelling wave? (Where rho is density, omega is angular frequency, A is amplitude)
View SolutionA 200Hz wave with amplitude 1mm travels on a long string of linear mass density 6g/m keep under a tension of 60N.
(a) Find the average power transmitted across a given point on the string.
(b) Find the total energy associated with the wave in a 2.0m long portion of the string.
View SolutionA 200Hz wave with amplitude 1mm travels on a long string of linear mass density 6g/m keep under a tension of 60N.
(a) Find the average power transmitted across a given point on the string.
(b) Find the total energy associated with the wave in a 2.0m long portion of the string.
View SolutionA transverse wave of amplitude 0.50 mm and frequency 100 Hz is produced on a wire stretched to a tension of 100 N. If the wave speed is 100 m s^-1, what average power is the source transmitting to the wire ?
View SolutionA trasverse wave of amplitude 0.50mm and frequency 100Hz is produced on a wire stretched to a tension of 100N. If the wave speed is 100m/s. What average power is the source transmitting to the wire?
View SolutionA standing wave pattern of maximum amplitude 2 mm is obtained in a string whose shape at t = 0 is represented in the graph.
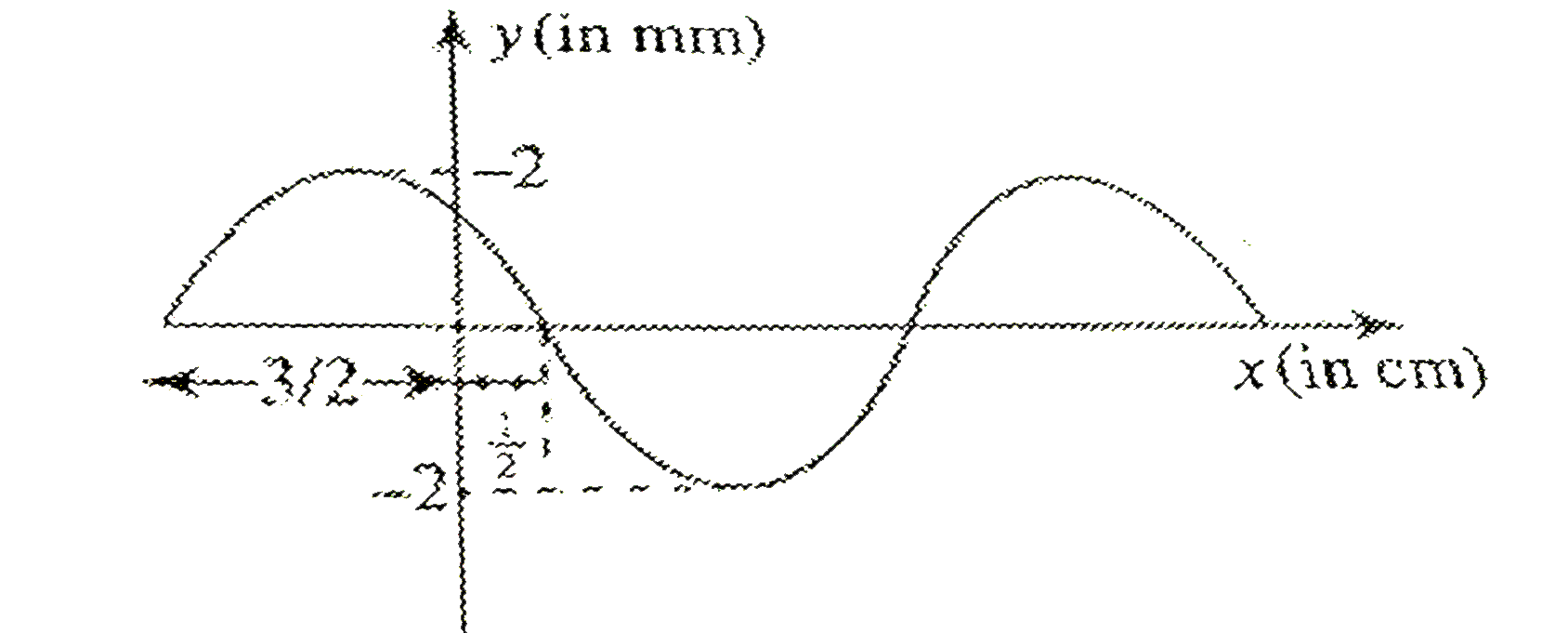
If the speed of the travelling wave in the string is 5 cm/s, then find the component waves.
View SolutionThe equation of a transverse wave travelling along x-axis is given by y = 10 sin π= (0.01 x- 2.0t) where y and x are represented in centimeters and, in seconds. Find the amplitude, frequency velocity and wavelength of the wave.
View Solution

