A taut string having tension 100 N and linear mass density 0.25kg/m is used inside a cart to generate a wave pulse starting at the left end, as shown. What should be the velocity of the cart so that pulse remains stationary w.r.t. ground.
To solve the problem, we need to find the velocity of the cart such that the wave pulse generated on the string remains stationary with respect to the ground. Here’s a step-by-step breakdown of the solution:
Step 1: Calculate the velocity of the wave pulse on the string
The velocity of a wave on a string can be calculated using the formula:
v=√Tμ
where:
- T is the tension in the string (in Newtons),
- μ is the linear mass density of the string (in kg/m).
Given:
- T=100N
- μ=0.25kg/m
Substituting the values into the formula:
v=√1000.25=√400=20m/s
Step 2: Relate the velocities of the pulse and the cart
To keep the wave pulse stationary with respect to the ground, the following relationship holds:
vpulse (ground)=vpulse (cart)+vcart (ground)
Since we want the pulse to be stationary with respect to the ground, we set:
vpulse (ground)=0
Thus, we have:
0=vpulse (cart)+vcart (ground)
Step 3: Substitute the known values
From Step 1, we know:
vpulse (cart)=20m/s
Substituting this into the equation gives:
0=20+vcart (ground)
Step 4: Solve for the velocity of the cart
Rearranging the equation to find the velocity of the cart:
vcart (ground)=−20m/s
Conclusion
The velocity of the cart should be 20m/s in the direction opposite to that of the wave pulse to ensure that the pulse remains stationary with respect to the ground.
The velocity of a wave on a string can be calculated using the formula:
v=√Tμ
where:
- T is the tension in the string (in Newtons),
- μ is the linear mass density of the string (in kg/m).
- T=100N
- μ=0.25kg/m
v=√1000.25=√400=20m/s
To keep the wave pulse stationary with respect to the ground, the following relationship holds:
vpulse (ground)=vpulse (cart)+vcart (ground)
Since we want the pulse to be stationary with respect to the ground, we set:
vpulse (ground)=0
0=vpulse (cart)+vcart (ground)
From Step 1, we know:
vpulse (cart)=20m/s
Substituting this into the equation gives:
0=20+vcart (ground)
Rearranging the equation to find the velocity of the cart:
vcart (ground)=−20m/s
The velocity of the cart should be 20m/s in the direction opposite to that of the wave pulse to ensure that the pulse remains stationary with respect to the ground.
Topper's Solved these Questions
- WAVE ON STRING Book:RESONANCE ENGLISHChapter:WAVE ON STRING Exercise:Solved Miscellaneous Problems
Explore 7 Videos
- WAVE ON STRING Book:RESONANCE ENGLISHChapter:WAVE ON STRING Exercise:Board Level Exercise
Explore 27 Videos
- TRAVELLING WAVESBook:RESONANCE ENGLISHChapter:TRAVELLING WAVESExercise:Exercise- 3 PART I
Explore 19 Videos
- WAVE OPTICSBook:RESONANCE ENGLISHChapter:WAVE OPTICSExercise:Advanced Level Problems
Explore 8 Videos
Similar Questions
A string of length 20cm and linear mass density 0.40g/cm is fixed at both ends and is kept under a tension of 16N.A wave pulse is produced at t=0 nearj an end as shown in figure which travels towards the other end.
when will the string have the shape shown in the figure again? (∈×10−2s)
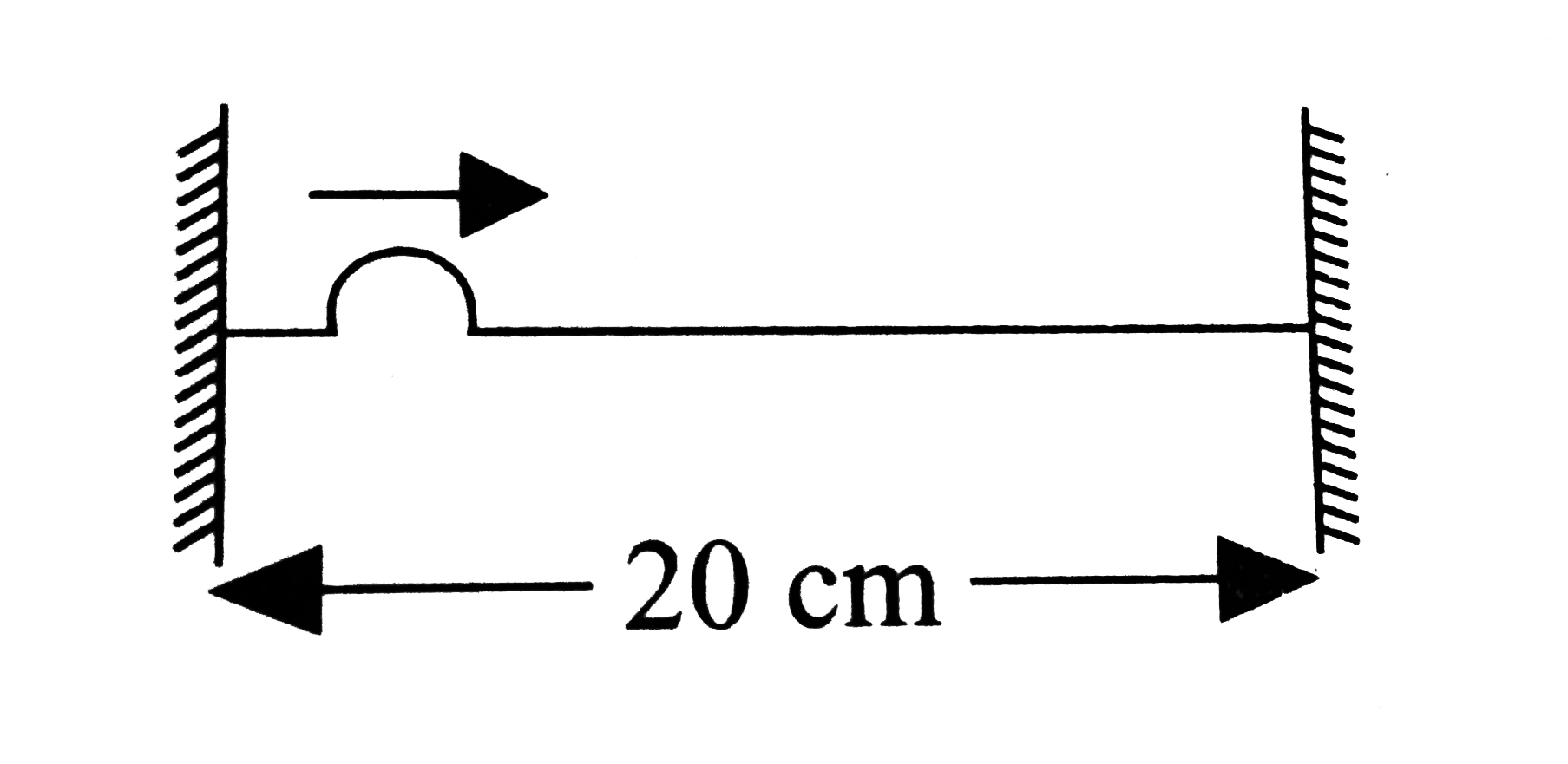
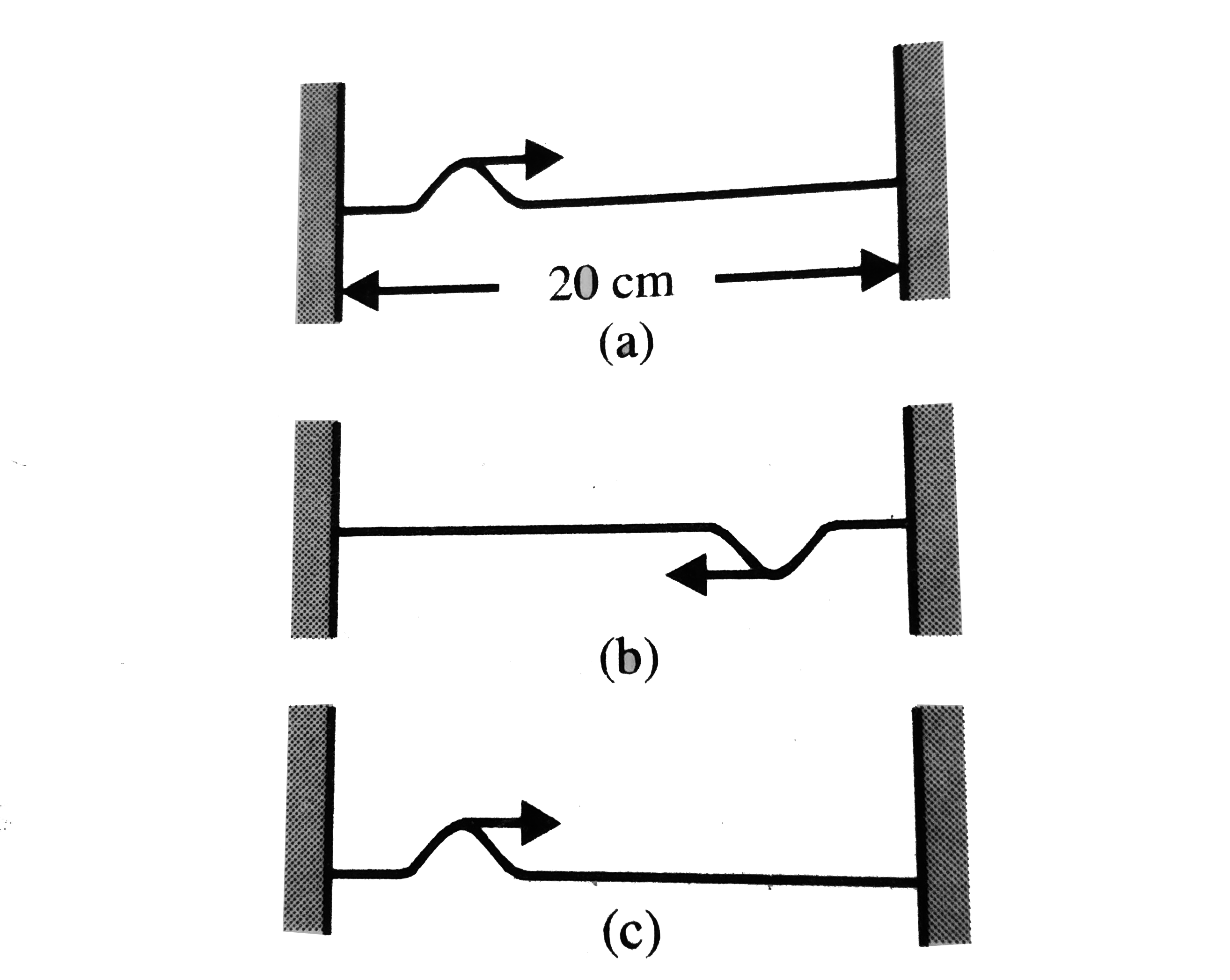
View SolutionA string of length 20cm and linear mass density 0.40g/cm is fixed at both ends and is kept under a tension of 16N . A wave pulse is produced at t=0 near an ends as shown in Fig. 7.17 (b) , which travels towards the other end . When will the string have the shape shown in the Fig . ( c).
View SolutionA 1m long wire having tension of 100 N and of linear mass density 0.01 kg/m is fixed and A and free at end B. the point C which is 20cm from end B is constrained to be stationary. To create resonance in the wire, the minimum frequency of the tuning fork will be :
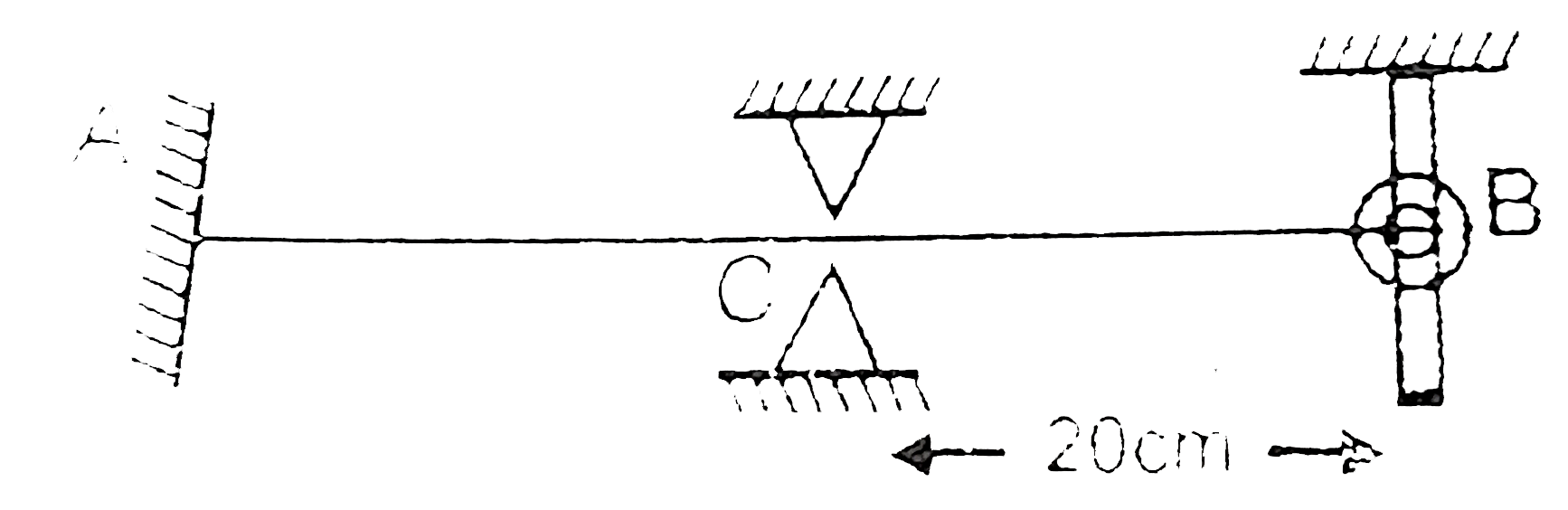
View SolutionFigure shown a clamped metal string of length 30cm and linear mass density 0.1kg/m. Which is taut at a tension of 40N. A small rider ( piece of paper ) is placed on string at point P as shown. An external vibrating tuning fork is brought near this string and oscillations of rider are carefully observed.
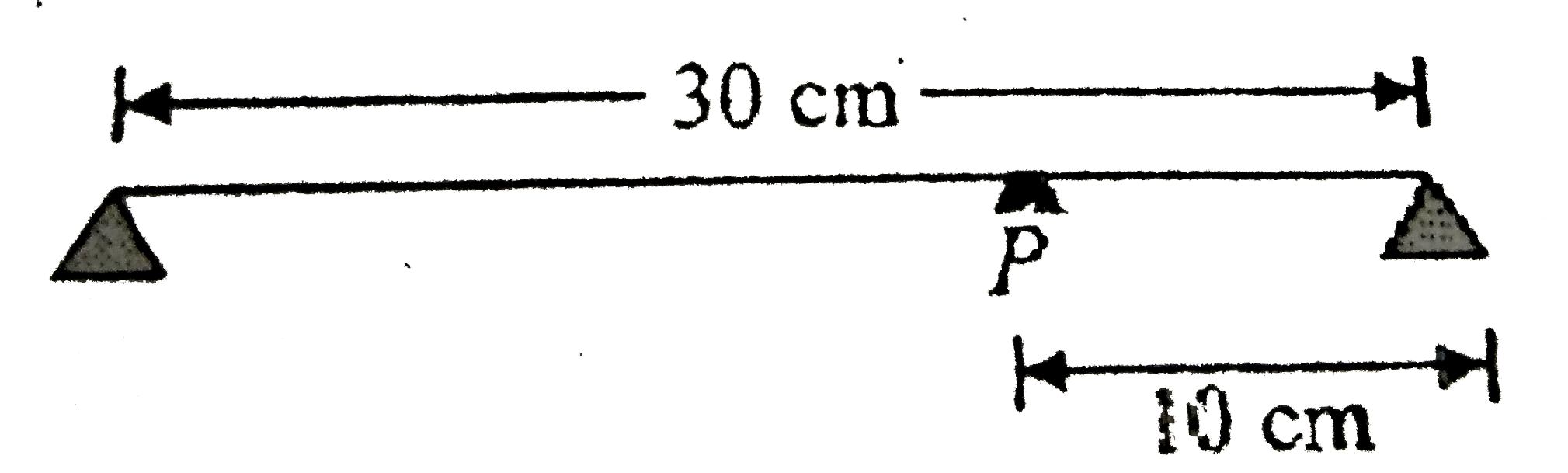
Now if the tension in the string is made 160N, at which of the following frequencies of turning fork , rider will not vibrate at all
View SolutionFigure shown a clamped metal string of length 30cm and linear mass density 0.1kg/m. Which is taut at a tension of 40N. A small rider ( piece of paper ) is placed on string at point P as shown. An external vibrating tuning fork is brought near this string and oscillations of rider are carefully observed.
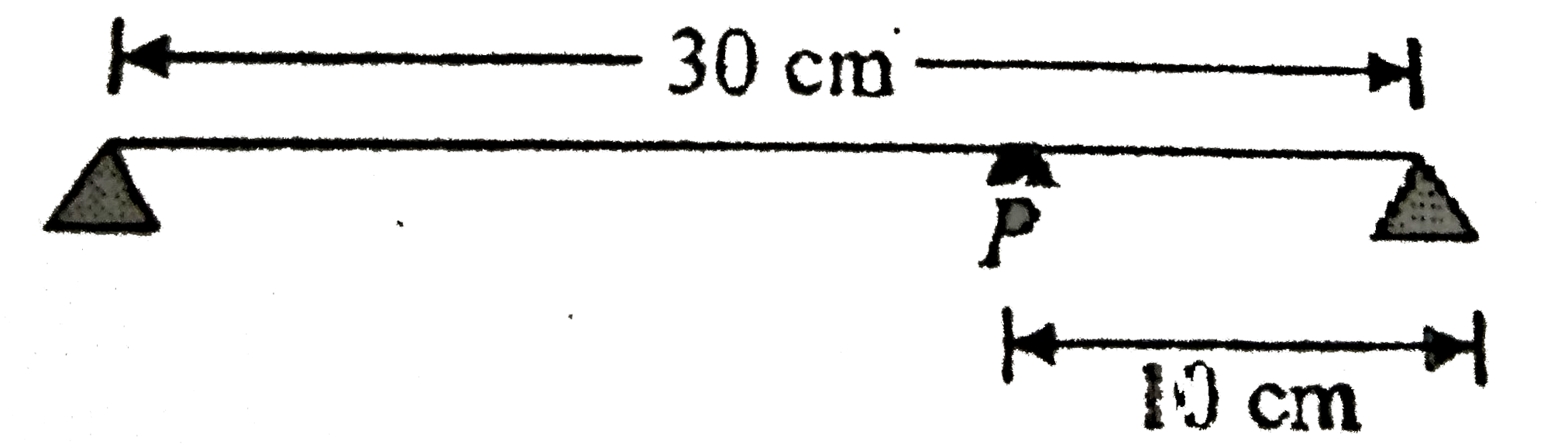
At which of the following frequencies the point P on string will have maximum oscillation amplitude among all points on string :
View SolutionA large mass M and a small mass m hang at the two ends of string that passes through a smooth tube as shown in fig. The mass m moves around in a circular path which lies in a horizantal plane. The length of the string from the mass m to the top of the tube is of length l and θ is the angle this length makes with the vertical, what should be the frequency of rotation of the mass m so that M remains stationary if M=16kg,m=4kg,l=1m and g=π2m/s2
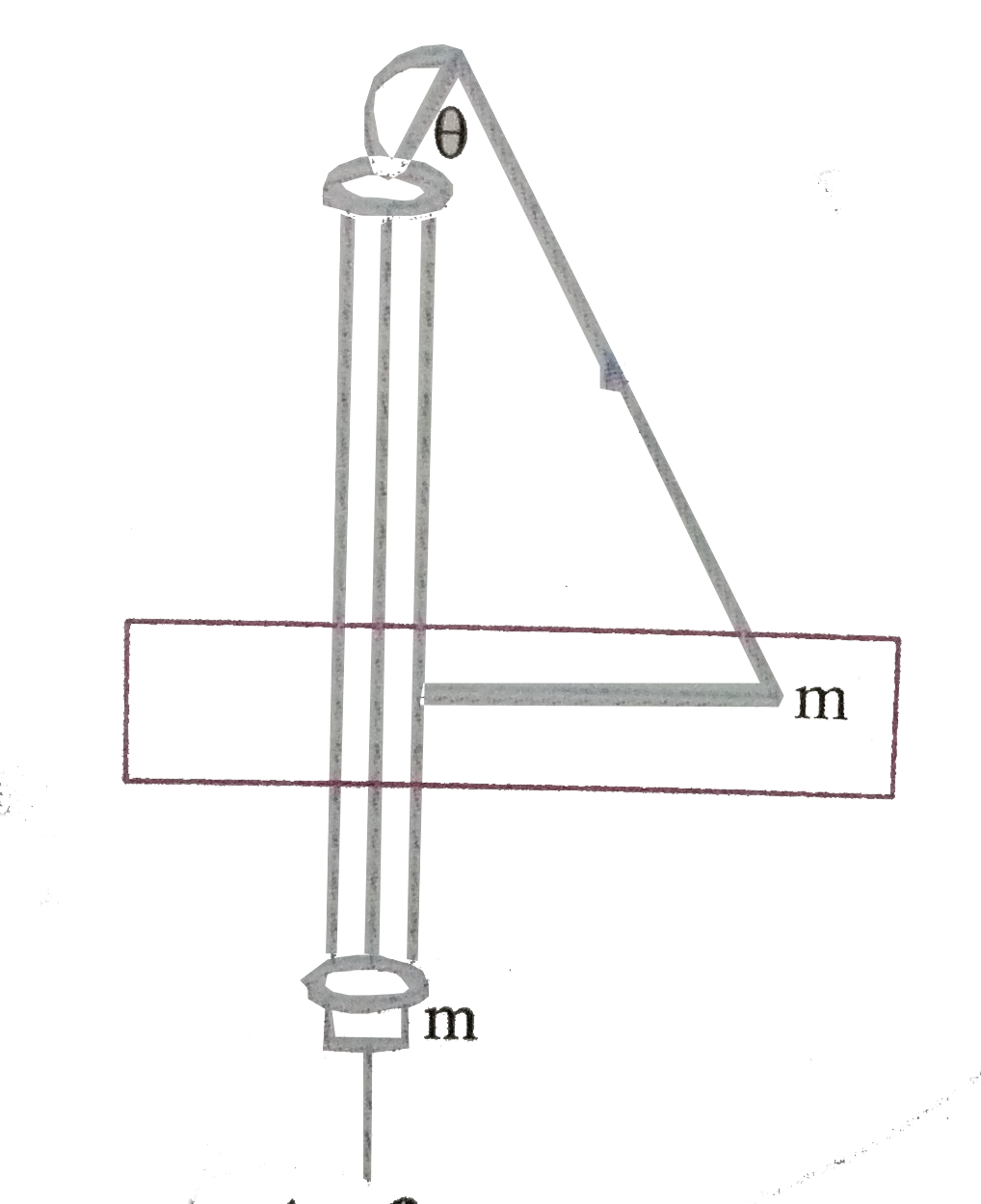
View SolutionTwo long strings A and B, each having linear mass density 1.2×10−2kgm−1, are stretched by different tensions 4.8 N and 7.5 N respectively and are kept parallel to each other with their left ends at x = 0. Wave pulses are produced on the strings at the left ends at t = 0 on string A and at t = 20 ms on string B. When and where will the pulse on B overtake that on A ?
View SolutionTwo uniform thin rods A and B of length 0.6 m each and of masses 0.01 kg and 0.02kg respectively are rigidly joined end to end. The combination is pivoted at the lighter end, P as shown in fig. Such that it can freely rotate about point P in a vertical plane. A small object of mass 0.05kg, moving horizontally, hits the lower end of the combination and sticks to it what should be the velocity of the object so that the system could just be reised to the horizontal position.
View SolutionThe pulse shown in figure has a speed of 10cm/s .

(a) If the linear mass density of the right string is 0.25 that of the left string, at what speed does the transmitted pulse travel?
(b) Compare the heights of the transmitted pulse and the reflected pulse to that of the incident pulse.
View SolutionA string of linear mass density 0.5gcm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end. The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20cms−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to regain its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string ?

View Solution

