At 0.04 M concentration, the molar conductivity of solution of an electrolyte is 5000Ω−1cm2mol−1 while at 0.01 M concentration the value is 5100Ω−1cm2mol−1. Making necessary assumption (Taking it as strong electrolyte) find the molar conductivity at infinite dilution and write percentage dissociation of strong electrolyte at 0.04 M.
The correct Answer is:96
To solve the problem, we need to find the molar conductivity at infinite dilution and the percentage dissociation of a strong electrolyte at a concentration of 0.04 M. Let's break down the steps:
Step 1: Understand the relationship between molar conductivity and concentration
For a strong electrolyte, the molar conductivity (Λ) versus the square root of concentration (√C) graph is a straight line. The equation of a straight line can be expressed as:
y=mx+c
where:
- y is the molar conductivity (Λ)
- x is the square root of concentration (√C)
- m is the slope
- c is the y-intercept (which represents the molar conductivity at infinite dilution)
Step 2: Calculate √C for the given concentrations
- For 0.04 M concentration:
√0.04=0.2
- For 0.01 M concentration:
√0.01=0.1
Step 3: Set up the equations based on the given data
From the problem, we have:
1. At 0.04 M:
5000=m(0.2)+c (Equation 1)
2. At 0.01 M:
5100=m(0.1)+c (Equation 2)
Step 4: Solve the equations simultaneously
We can rearrange both equations to isolate c:
1. From Equation 1:
c=5000−0.2m
2. From Equation 2:
c=5100−0.1m
Now, set the two expressions for c equal to each other:
5000−0.2m=5100−0.1m
Step 5: Solve for m
Rearranging gives:
0.1m=5100−5000
0.1m=100
m=1000
Step 6: Substitute m back to find c
Using m=1000 in Equation 1:
c=5000−0.2(1000)
c=5000−200
c=4800
Step 7: Determine molar conductivity at infinite dilution
The y-intercept c represents the molar conductivity at infinite dilution:
Λ∞=4800Ω−1cm2mol−1
Step 8: Calculate the degree of dissociation (α)
The degree of dissociation (α) can be calculated using the formula:
α=ΛΛ∞
Where:
- Λ is the molar conductivity at the given concentration (0.04 M), which is 5000 Ω−1cm2mol−1.
Substituting the values:
α=50004800
α≈1.04167
Step 9: Convert to percentage
To find the percentage dissociation:
Percentage dissociation=α×100
Percentage dissociation≈104.17%
Since this value exceeds 100%, we need to ensure that we interpret this correctly. For strong electrolytes, this indicates that the electrolyte is fully dissociated, and we can state that the percentage dissociation is effectively 100%.
Final Answers
- Molar conductivity at infinite dilution: 4800Ω−1cm2mol−1
- Percentage dissociation at 0.04 M: 100%
For a strong electrolyte, the molar conductivity (Λ) versus the square root of concentration (√C) graph is a straight line. The equation of a straight line can be expressed as:
y=mx+c
where:
- y is the molar conductivity (Λ)
- x is the square root of concentration (√C)
- m is the slope
- c is the y-intercept (which represents the molar conductivity at infinite dilution)
- For 0.04 M concentration:
√0.04=0.2
- For 0.01 M concentration:
√0.01=0.1
From the problem, we have:
1. At 0.04 M:
5000=m(0.2)+c (Equation 1)
2. At 0.01 M:
5100=m(0.1)+c (Equation 2)
We can rearrange both equations to isolate c:
1. From Equation 1:
c=5000−0.2m
2. From Equation 2:
c=5100−0.1m
5000−0.2m=5100−0.1m
Rearranging gives:
0.1m=5100−5000
0.1m=100
m=1000
Using m=1000 in Equation 1:
c=5000−0.2(1000)
c=5000−200
c=4800
The y-intercept c represents the molar conductivity at infinite dilution:
Λ∞=4800Ω−1cm2mol−1
The degree of dissociation (α) can be calculated using the formula:
α=ΛΛ∞
Where:
- Λ is the molar conductivity at the given concentration (0.04 M), which is 5000 Ω−1cm2mol−1.
α=50004800
α≈1.04167
To find the percentage dissociation:
Percentage dissociation=α×100
Percentage dissociation≈104.17%
- Molar conductivity at infinite dilution: 4800Ω−1cm2mol−1
- Percentage dissociation at 0.04 M: 100%
Topper's Solved these Questions
Similar Questions
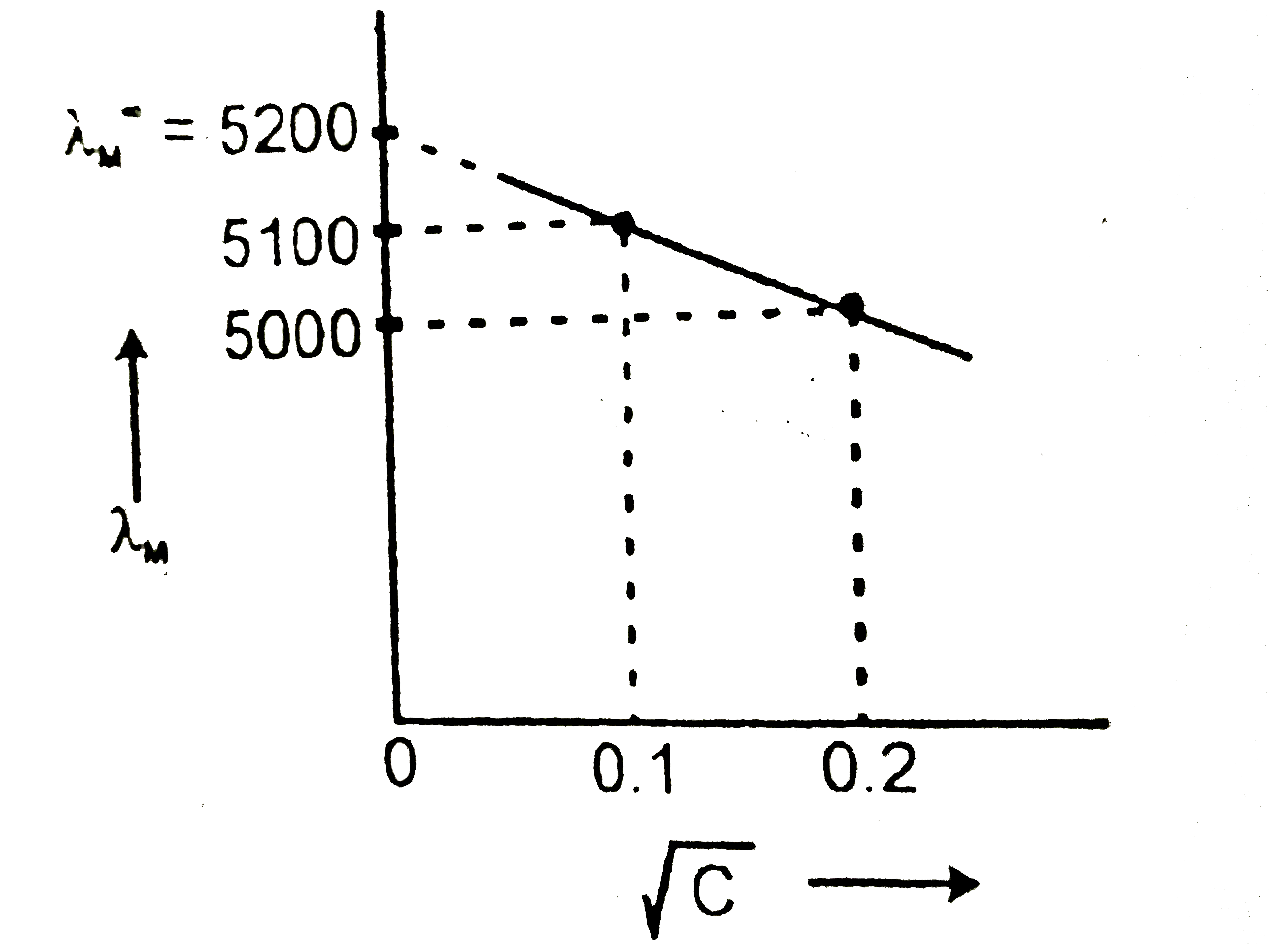
At 0.04 M concentration the molar conductivity of a solution of a electrolyte is 5000Ω−1cm2mol−1 while at 0.01 M concentration the value is 5100Ω−1cm2mol−1 making necessary assumption (taking it as strong electrolyte) find the molar conductivity at infinite dilution and also determine the degree of dissociation of strong electrolyte at 0.04M.
View SolutionThe molar conductivity of 0.05 M solution of weak acid is 16.6Ω−1cm−2mol−1. Its molar conductivity at infinite dilution is 390.7Ω−1cm−2mol−1. The degree of dissociation of weak acid is
View Solution
Knowledge Check
Molar conductivity of 0.15 M solution of KCI at 298 K, if its conductivity is 0.0152 S cm−1 will be
A124Ω−1cm2mol−1B204Ω−1cm2mol−1C101Ω−1cm2mol−1D300Ω−1cm2mol−1
The molar conductivity of a 1.5 M solution of an electrolyte is found to be 138.9Scm2mol−1 . Calculate the conductivity of this solution.
View SolutionThe molar conductivity of a 1.5 M solution of an electrolyte is found to be 138.9Scm2mol−1 . Calculate the conductivity of this solution.
View SolutionThe equivalent conductivity of 0.1M weak acid is 100 times less than that at infinite dilution. The degree of dissociation of weak electrolyte at 0.1M is.
View SolutionThe molar conductance at infinite dilution for electrolytes BA and CA are 140 and 120 ohm−1Cm2mol−1 respectively. If the molar conductance at infinite dilution of BX is 198 ohm−1cm2mol−1, then then at infinite dilution, the molar conductance of is:
View SolutionThe equivalent conductance of a 0.2 n solution of an electrolyte was found to be 200Ω−1cm2eq−1 . The cell constant of the cell is 2cm−1 . The resistance of the solution is
View SolutionIf a centi normal solution of NH4OH has molar conductivity equal to 9.6Ω−1cm2mol−1. what will be the per cent dissociation of NH4OH at this dilution.
View SolutionThe conductivity of 0.35M solution of KCl at 300K is 0.0275 S cm−1. Calculate molar conductivity
View Solution