If we use very thin and long wire, then
Sensitivity (output/input=ΔX/ΔW) of experiment increases
Young's modulus will remain unchanged
Wire may break or yield during loading.
All of the above
To solve the question regarding the effects of using a very thin and long wire, we will analyze the concepts of sensitivity, Young's modulus, and the potential for the wire to break or yield under loading conditions.
1. Understanding Sensitivity:
- Sensitivity (S) is defined as the ratio of the change in output (Δx) to the change in input (ΔW), i.e., S=ΔxΔW.
- In this context, Δx represents the change in length of the wire (ΔL) when a weight (ΔW) is applied.
2. Relating Stress and Strain:
- Stress (σ) is defined as the force (F) applied per unit area (A), i.e., σ=FA.
- Strain (ε) is defined as the change in length (ΔL) per original length (L), i.e., ϵ=ΔLL.
- Young's modulus (E) is given by the ratio of stress to strain, E=σϵ.
3. Calculating Stress:
- For a wire of diameter D, the area A can be expressed as A=πD24.
- Therefore, the stress can be rewritten as σ=ΔWπD24=4ΔWπD2.
4. Calculating Strain:
- The strain can be expressed as ϵ=ΔLL.
5. Expressing Young's Modulus:
- Substituting the expressions for stress and strain into the Young's modulus formula gives:
E=σϵ=4ΔWπD2ΔLL=4LΔWπD2ΔL
6. Analyzing Sensitivity with Length:
- If we increase the length of the wire (L), the sensitivity S can be expressed as:
S=ΔLΔW=4LπD2E
- As L increases, the sensitivity S increases as well.
7. Considering Young's Modulus:
- Young's modulus is a material property and does not change with the dimensions of the wire. Thus, it remains unchanged regardless of the wire's length or thickness.
8. Potential for Wire to Break or Yield:
- A very thin wire may have a lower tensile strength. If the applied weight exceeds the tensile strength of the wire, it may break or yield.
Conclusion:
Based on the analysis:
- Sensitivity increases with the length of the wire.
- Young's modulus remains unchanged.
- The wire may break or yield under excessive loading.
Thus, all options provided in the question are correct.
- Sensitivity (S) is defined as the ratio of the change in output (Δx) to the change in input (ΔW), i.e., S=ΔxΔW.
- In this context, Δx represents the change in length of the wire (ΔL) when a weight (ΔW) is applied.
- Stress (σ) is defined as the force (F) applied per unit area (A), i.e., σ=FA.
- Strain (ε) is defined as the change in length (ΔL) per original length (L), i.e., ϵ=ΔLL.
- Young's modulus (E) is given by the ratio of stress to strain, E=σϵ.
- For a wire of diameter D, the area A can be expressed as A=πD24.
- Therefore, the stress can be rewritten as σ=ΔWπD24=4ΔWπD2.
- The strain can be expressed as ϵ=ΔLL.
- Substituting the expressions for stress and strain into the Young's modulus formula gives:
E=σϵ=4ΔWπD2ΔLL=4LΔWπD2ΔL
- If we increase the length of the wire (L), the sensitivity S can be expressed as:
S=ΔLΔW=4LπD2E
- As L increases, the sensitivity S increases as well.
- Young's modulus is a material property and does not change with the dimensions of the wire. Thus, it remains unchanged regardless of the wire's length or thickness.
- A very thin wire may have a lower tensile strength. If the applied weight exceeds the tensile strength of the wire, it may break or yield.
Based on the analysis:
- Sensitivity increases with the length of the wire.
- Young's modulus remains unchanged.
- The wire may break or yield under excessive loading.
Topper's Solved these Questions
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Exercise
12 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Exercise -1 PART
1 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems
35 Videos
Similar Questions
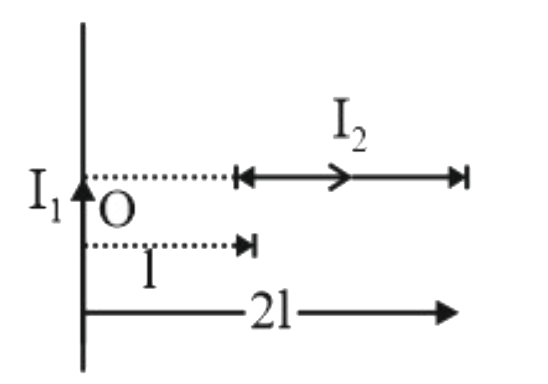
A finite carrying - current wire is placed in a plane along with very long ,straight conductor carrying current as shown in the figure. The torque on the finite current wire about point O is
View SolutionIn which stage the chromosomes appear thin and long thread-like
View Solution(a) Name two factors on which the specific resistance of a wire depends ?
(b) Two wires A and B are made of copper. The wire A is long and thin, while the wire B is short and thick. Which will have more specific resistance ?
View SolutionThe region of the root consisting of very small, thin walled cells with dense protoplasm
View SolutionIn a transistor the base is made very thin and is lightly doped with an impurity, because.
View SolutionA part of circuit is shown in figure . The wire A is a very thick copper and wire B and C are identical wires of manganin . The currents in wire A , B , C will be respectively

View SolutionIn order to have a current in a long wire, it should be
connected to a battery or some such device. Can we
obtain the magnetic field due to a straight, long wire by
using Ampere's law without mentioning this other part of the circuit?
View SolutionA circular coil of wire carries a current . PQ is a part of very long wire carrying a current and passing close to the circular coil. If the direction of currents are those shown in figure, then the direction of the force acting on PQ is

View SolutionA junction diode , in which one of the p or n - sections is made very thin, can be used to convert light energy into electrical energy, then the diode is called
View SolutionAfter taking a long breath, we can hold the breath as long as
View Solution
