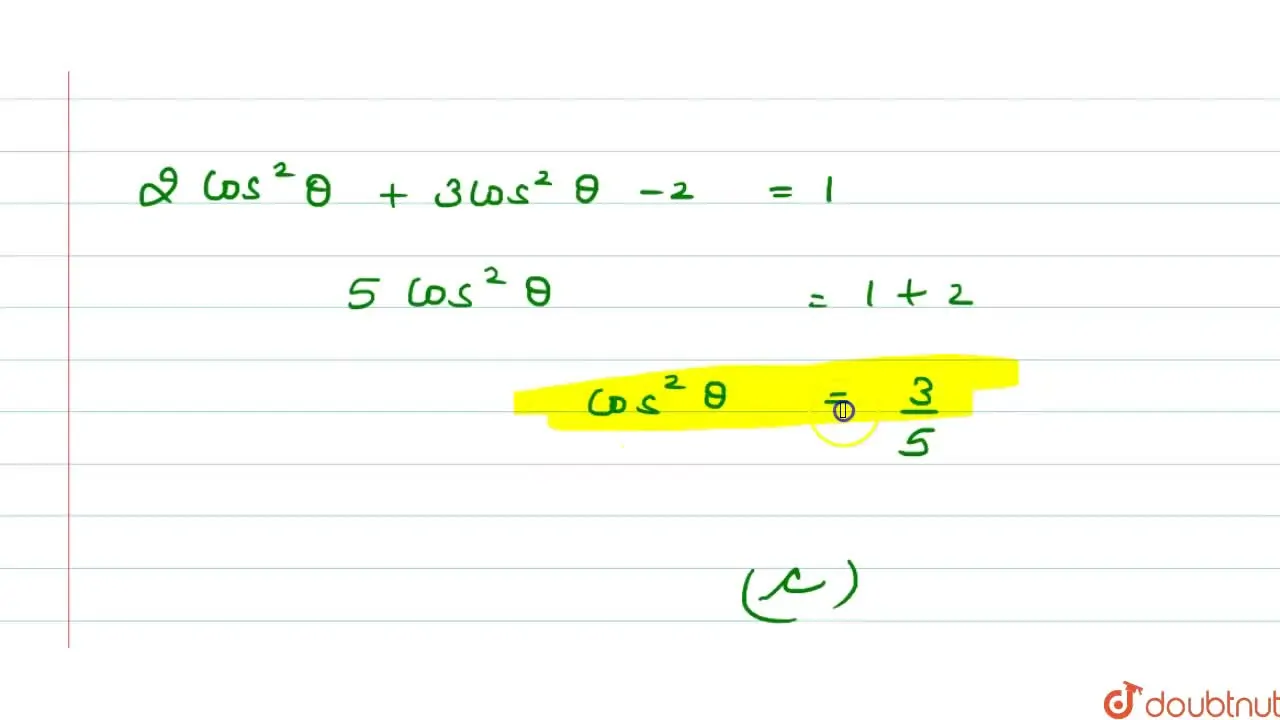A line makes an angle θ with each of the x-and z-axes. If the angle β, which it makes with the y-axis, is such that sin2β=3sin2θ,thencos2θ equals a. 23 b. 15 c. 35 d. 25
23
1√2
12
Data inappropriate
The correct Answer is:C
A line makes angle θ with x-axis and z-axis and β with y-axis.
∴l=cosθ,m=cosβ,n=cosθ
∵l2+m2+n2=1
∴cos2θ+cos2β+cos2θ=1
⇒2cos2θ=1−cos2β
⇒2cos2θ=sin2β
But, it is given
sin2β=2sin2θ
Form Eqs i and ii we get
2sin2θ=2cos2θ
⇒tan2θ=1⇒cos2θ=12
Related Playlists
Similar Questions
A line makes an angel θ with each of the x-and z-axes. If the angel β, which it makes with the y-axis, is such that sin2β=3sin2θ,then cos2θ equals a. 23 b. 15 c. 35 d. 25
View SolutionA line makes the same angle θ with X-axis and Z-axis. If the angle β, which it makes with Y-axis, is such that sin2(β)=3sin2θ, then the value of cos2θ is
View SolutionA line makes an angle θ with the x-axis and the y-axis. If it makes an angle α with the z - axis such that sin2α=3sin2θ, then cos2θ is equal to
View SolutionIf sec4θ+sec2θ=10+tan4θ+tan2θ, then sin2θ= 23 (b) 34 (c) 45 (d) 56
View SolutionProve that: sinθ−12sin2θ+13sin3θ−…→∞=θ2
View SolutionIf cosecθ−cotθ=12,0<θ<π2 then cosθ= a.53,b.35,c.−35,d.−53
View SolutionIf cosecθ−cotθ=12,0<θ<π2 then cosθ= a.53,b.35,c.−35,d.−53
View SolutionProve that : cos2θ+sin2θcos2β=cos2β+sin2βcos2θ
View SolutionThe maximum value of the expression 1sin2θ+3sinθcosθ+5cos2θ is
View SolutionThe maximum value of the expression 1sin2θ+3sinθcosθ+5cos2θ is
View Solution