The work done an a particle of mass by a force
(K being a constant of appropriate dimensions), when the partical is taken from the point (a,0) to the point (0,a) along a circular path of radius a about the origin in x - y plane is
zero
none
The correct Answer is:B
This force is tangential and constant magnitude done will be product of force and distance.
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
Find the distance of the point (2,3) from the line 2x−3y+9=0 measured along a line x−y+1=0.
View SolutionThe maximum distance of the point (k,0) from the curve 2x2+y2−2x=0 is equal to
View SolutionIf the points (2, 1) and (1, −2) are equidistant from the point (x, y) , show that x+3y=0 .
View SolutionThe work done by the force F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown in
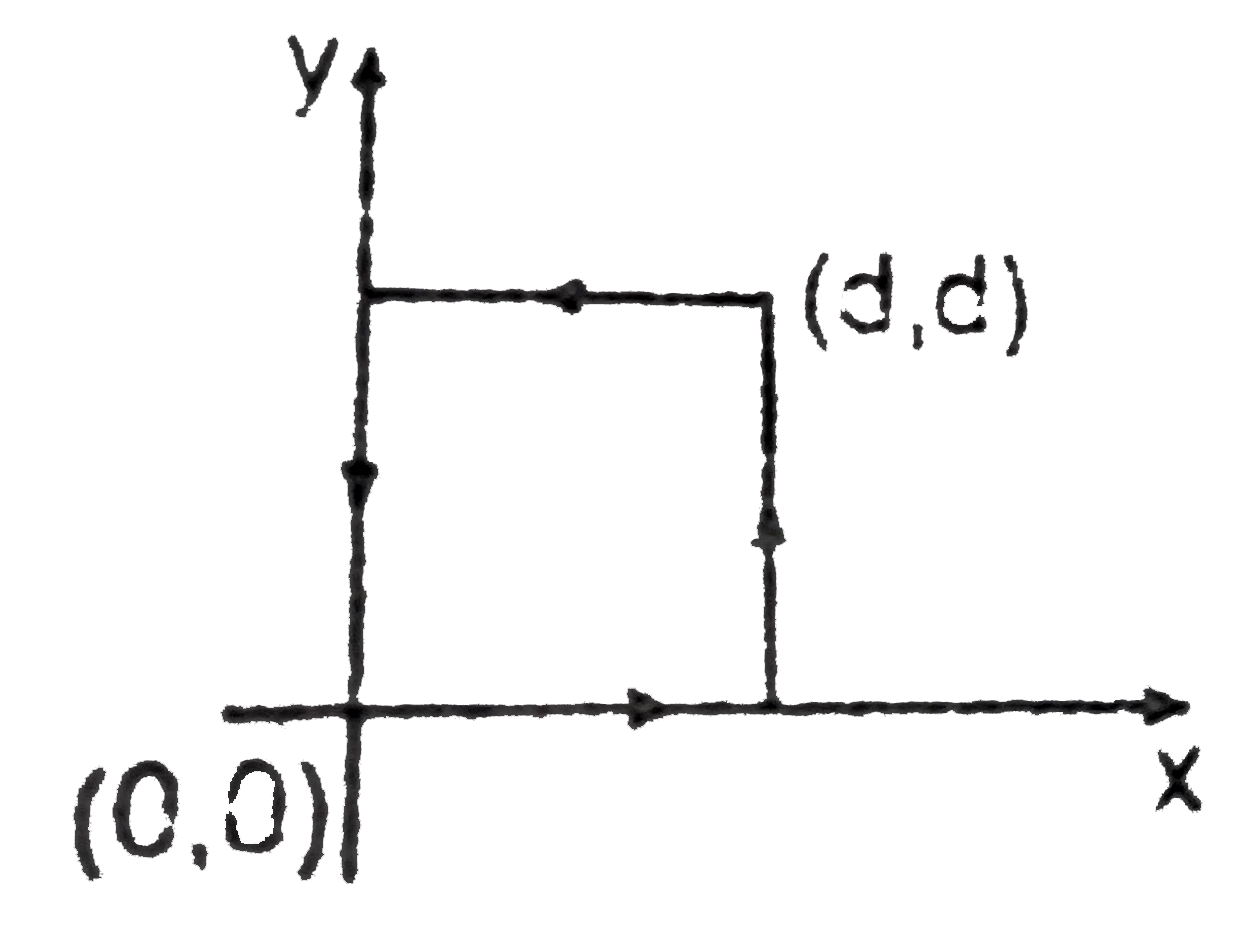
View SolutionA force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
View SolutionFind what the following equation become when the origin is shifted to the point (1,1): x2+xy−3x−y+2=0
View SolutionA particle of mass m and charge q is in a electric and magnetic field given by
→E=2ˆi+3ˆj,→B=4ˆj+6ˆk
The charged particle is shifted form the origin to the point P(x = 1, y=1) along a striaght path. The magnitude of the total work done is :
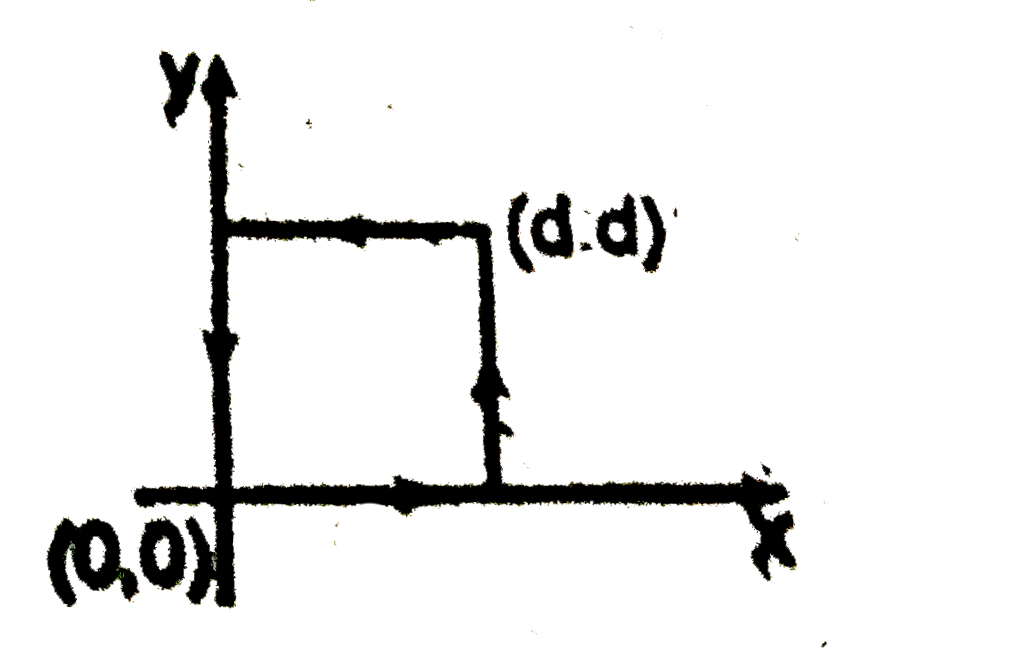
View SolutionThe work done by the force →F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown is :
View SolutionThe distance of the point (1,−2,4) from the plane passing through the point (1,2,2) perpendicular to the planes x−y+2z=3 and 2x−2y+z+12=0 is
View SolutionA particle is moved inx−y plane form (a,0) to (0,a) along circular arc having centre at origin. Work done by a force −ky(x2+y2)32ˆi+kx(x2+y2)32ˆj on the particle during this motion will be
View Solution
