A source which is emitting sound of frequency f is initially at (−r,0) and an observer is situated initally at (2r,0). If observer and source both are moving with velocities →vobserver=−√2Vˆi−√2ˆj and →vsource=V√2ˆi+V√2ˆj, then which of the following is correct option ?
Apparent frequency first increases, then decreases and observer the original frequency once during the motion.
Apparent frequency first increases, then decreases and observer the original frequency twice during the motion.
Apparent frequency first increases, then decreases during the motion and observer never observer the initial frequency.
Apparent frequency continously decreases and one during the motion, observer hears the original frequency.
The correct Answer is:D
To solve the problem, we need to analyze the motion of both the source and the observer, and how their velocities affect the apparent frequency of the sound they perceive.
1. Identify Initial Positions and Velocities:
- The source is at position (−r,0) and emits sound with frequency f.
- The observer is at position (2r,0).
- The velocity of the observer is given as →vobserver=−√2V^i−√2V^j.
- The velocity of the source is given as →vsource=V√2^i+V√2^j.
2. Determine the Direction of Motion:
- The observer is moving towards the origin (left and down), while the source is moving towards the first quadrant (up and right).
- This means that the observer and the source are moving towards each other.
3. Calculate the Relative Velocities:
- The relative velocity of approach between the observer and the source can be calculated by adding their velocities since they are moving towards each other.
- The relative velocity vrelative=→vobserver−→vsource.
4. Determine the Apparent Frequency:
- The apparent frequency f′ can be calculated using the Doppler effect formula:
f′=f(v+vobserverv−vsource)
- Here, v is the speed of sound, vobserver is the component of the observer's velocity towards the source, and vsource is the component of the source's velocity towards the observer.
5. Analyze the Change in Apparent Frequency:
- As the observer approaches the source, the apparent frequency will increase.
- Once the observer reaches the closest point to the source, the frequency will start to decrease as the observer moves away.
6. Conclusion:
- The apparent frequency first increases as the observer approaches the source and then decreases as the observer moves away. The observer will hear the original frequency once during this motion when they are at the closest point to the source.
Final Answer:
The correct option is D: The apparent frequency continuously decreases, and once during the motion, the observer hears the original frequency.
- The source is at position (−r,0) and emits sound with frequency f.
- The observer is at position (2r,0).
- The velocity of the observer is given as →vobserver=−√2V^i−√2V^j.
- The velocity of the source is given as →vsource=V√2^i+V√2^j.
- The observer is moving towards the origin (left and down), while the source is moving towards the first quadrant (up and right).
- This means that the observer and the source are moving towards each other.
- The relative velocity of approach between the observer and the source can be calculated by adding their velocities since they are moving towards each other.
- The relative velocity vrelative=→vobserver−→vsource.
- The apparent frequency f′ can be calculated using the Doppler effect formula:
f′=f(v+vobserverv−vsource)
- Here, v is the speed of sound, vobserver is the component of the observer's velocity towards the source, and vsource is the component of the source's velocity towards the observer.
- As the observer approaches the source, the apparent frequency will increase.
- Once the observer reaches the closest point to the source, the frequency will start to decrease as the observer moves away.
- The apparent frequency first increases as the observer approaches the source and then decreases as the observer moves away. The observer will hear the original frequency once during this motion when they are at the closest point to the source.
The correct option is D: The apparent frequency continuously decreases, and once during the motion, the observer hears the original frequency.
Topper's Solved these Questions
- SOUND WAVESBook:RESONANCE ENGLISHChapter:SOUND WAVESExercise:Exercise- 2 PART - II
Explore 20 Videos
- SOUND WAVESBook:RESONANCE ENGLISHChapter:SOUND WAVESExercise:Exercise- 2 PART - III
Explore 19 Videos
- SOUND WAVESBook:RESONANCE ENGLISHChapter:SOUND WAVESExercise:Exercise- 1 PART - II
Explore 30 Videos
- SIMPLE HARMONIC MOTIONBook:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Exercise
Explore 28 Videos
- STRING WAVESBook:RESONANCE ENGLISHChapter:STRING WAVESExercise:Exercise
Explore 32 Videos
Similar Questions
The expression (1√2ˆi+1√2ˆj) is a
View SolutionA source of sound emitting a note of frequency 200 Hz moves towards an observer with a velocity v equal to the velocity of sound. If the observer also moves away from the source with the same velocity v, the apparent frequency heard by the observer is
View Solution
Knowledge Check
A vector parallel to the line of intersection of the planes →r(3ˆi−ˆj+ˆk)=5and→r(ˆi+4ˆj−2ˆk)=3 is
A2ˆi+7ˆj−13ˆkB2ˆi−7ˆi+13ˆkC−2ˆi+7ˆj+13ˆkD2ˆi+7ˆj+13ˆkThe angle between the lines →r=(4ˆi−ˆj)+λ(2ˆi+ˆj−3ˆk)and→r=(ˆi−ˆj+2ˆk)+μ(ˆi−3ˆj−2ˆk) is
Aπ6Bπ3Cπ4Dπ2
If →E=2x2ˆi−3y2ˆj, then V (x, y, z)
View SolutionIf →F=(60ˆi+15ˆj−3ˆk)N and →V=(2ˆi−4ˆj+5ˆk) m/s, then instantaneous power is:
View SolutionFor a body, angular velocity (→ω)=ˆi−2ˆj+3ˆk and radius vector (→r)=ˆi+ˆj+→k, then its velocity is :
View SolutionA particle of mass 2kg is moving with velocity →v0=(2ˆi−3ˆj)m/s in free space. Find its velocity 3s after a constant force →F=(3ˆi+4ˆj)N starts acting on it.
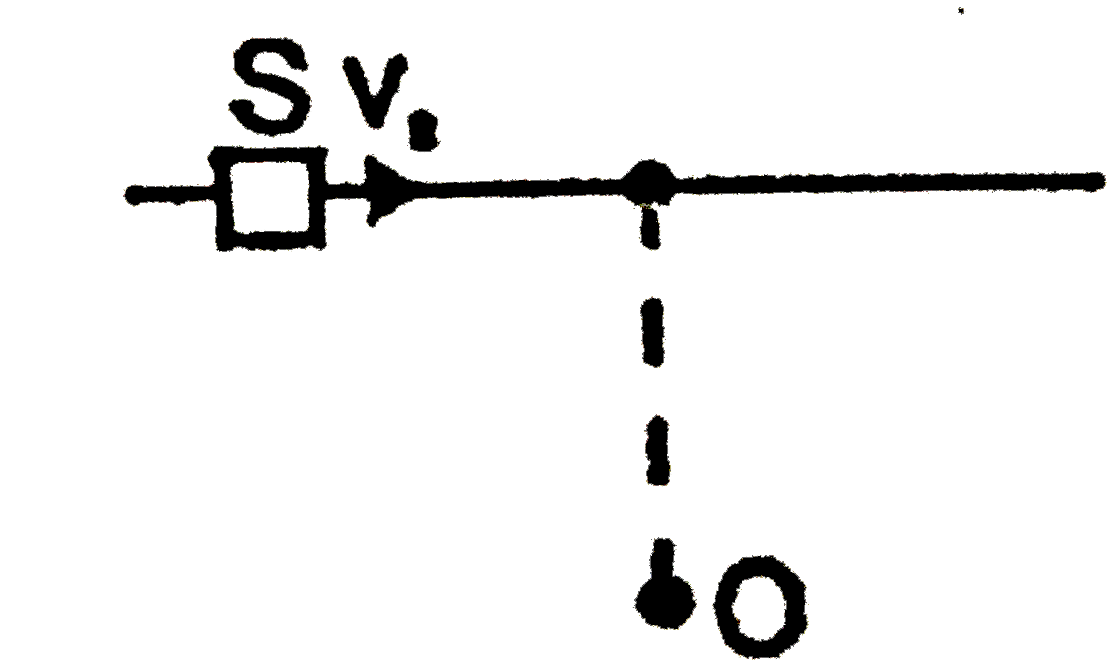
View SolutionThe source (S) of sound is moving constant velocity v0 as shown in diagram. An observer O listens to the sound emmited by the source. The observed frequency of the sound
View SolutionIf →E=2yˆi+2xˆj, then find V(x,y,z)
View Solution