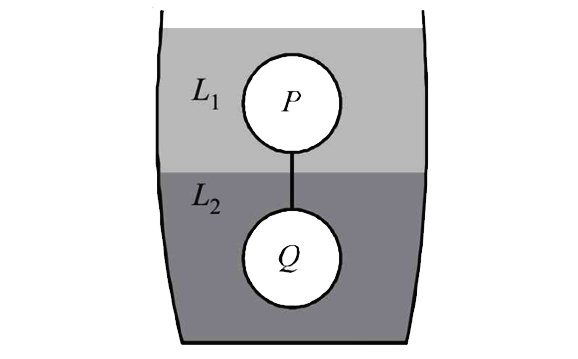
Two sphere P and Q for equal radii have densities ρ1andρ2 respectively. The spheres are connected by a massless string and placed in liquids L1andL2 of densities σ1andσ2 and viscosities η1andη2, respectively. They float in equilibrium with the sphere P in L1 and sphere Q in L2 and the string being taut (see figure). If sphere P alone in L2 has terminal velocity vP and Q along in L1 has terminal velocity vQ, then :

∣∣ ∣∣−→VP−→VQ∣∣ ∣∣=η1η2
∣∣ ∣∣−→VP−→VQ∣∣ ∣∣=η2η1
−→VP.−→VQ>0
→VP.→VQ<0
The correct Answer is:A, D
For floating
(ρ1+ρ2)V=(σ1+σ2)V
ρ1+ρ2=σ1+σ2
since strings in taut so
ρ1<σ1,ρ2>σ2
VP=29r2(σ2−ρ1)gη2
VQ=29(σ1−ρ2)gη1
since σ2−ρ1=−(σ1−ρ2)
∣∣∣VPVQ∣∣∣=η1η2
−→VP.−→VQ<0 because VP and VQ are oppsite

Topper's Solved these Questions
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Exercise- 3 PART - IV
9 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Exercise- 2 PART - III
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 92 illustration
2 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise
43 Videos
Similar Questions
Two spheres P and Q of equal radii have densities ρ1 and ρ2, respectively. The spheres are connected by a massless string and placed in liquids L1 and L2 of densities σ1 and σ2 and viscosities η1 and η2, respectively. They float in equilibrium with the sphere P in L1 and sphere Q in L2 and the string being taut(see figure). If sphere P alone in L2 has terminal velocity →Vp and Q alone in L1 has terminal velocity →VQ, then
View SolutionIf two liquids of same mass but densities ρ1 and ρ2 respectively are mixed, then the density of the mixture is:
View SolutionIf two liquids of same volume but different densities ρ1 and ρ2 are mixed, then the density of the mixture is:
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionTwo spheres A and B of equal radii R, each are uniformly dense with densities 2ρ and rho respectively are placed as shown in figure.The initial acceleration of particle placed at point P due to gravity of both the spheres will be (P is just above the surface of sphere B).
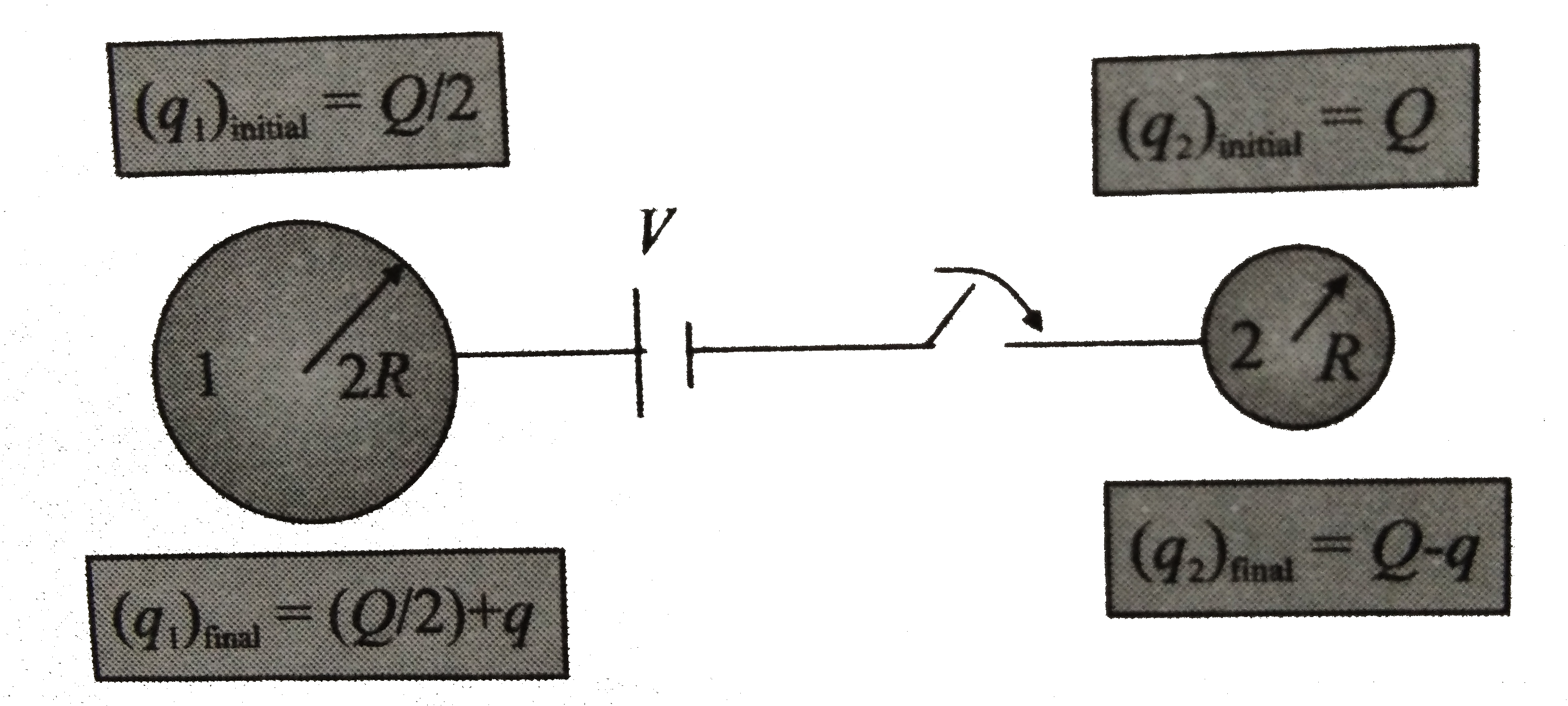
View SolutionThere are two spheres of radii R and 2R having charges Q and Q/2, respectively. These two spheres are connected with a cell of emf V volts as show in. When the switch is closed, find the final charge on each sphere.
View SolutionEqual masses of two substance of densities ρ1andρ2 are mixed together. What is the density of the mixture?
View SolutionA sphere of density ρ is half submerged in a liquid of density σ and surface tension T. The sphere remains in equilibrium. Find radius of the sphere (assume the force due to surface tension acts tangentially to surface of sphere)
View SolutionA metal sphere connected by a string is dipped in a liquid of density ρ as shown in figure. The pressure at the bottom of the vessel will be, (p0=atmospheric pressure )

View Solution
