A sphere is dropped gently into a medium of infinite extent. As the sphere falls, the force acting downwards on it.
remain constant throughout
increases for sometimes and then becomes constant
decreases for sometimes and then becomes zero
increases for sometime and then decreases.
The correct Answer is:D
To solve the problem of the forces acting on a sphere that is dropped gently into a medium of infinite extent, we can break down the situation step by step.
1. Understanding the Forces Acting on the Sphere:
When the sphere is dropped into the medium, two main forces act on it: the gravitational force (weight) acting downwards and the buoyant force acting upwards.
2. Gravitational Force:
The gravitational force (weight) acting on the sphere can be expressed as:
Fg=mg
where m is the mass of the sphere and g is the acceleration due to gravity.
3. Buoyant Force:
The buoyant force (Fb) acting on the sphere can be calculated using Archimedes' principle, which states that the buoyant force is equal to the weight of the fluid displaced by the sphere. It can be expressed as:
Fb=ρVg
where ρ is the density of the medium, V is the volume of the sphere, and g is the acceleration due to gravity.
4. Net Force Acting on the Sphere:
As the sphere falls, the net force (Fnet) acting on it can be expressed as:
Fnet=Fg−Fb
Initially, when the sphere is dropped, the buoyant force is less than the gravitational force, resulting in a downward acceleration.
5. Equilibrium Condition:
As the sphere continues to fall, it displaces more fluid, which increases the buoyant force. Eventually, the buoyant force will increase to equal the gravitational force. At this point, the sphere reaches a state of equilibrium, and the net force becomes zero:
Fg=Fb
This means that the sphere will stop accelerating and will fall at a constant velocity, known as terminal velocity.
6. Conclusion:
Thus, the force acting downwards on the sphere decreases as it falls due to the increasing buoyant force until it reaches equilibrium.
Final Answer:
The force acting downwards on the sphere decreases until it reaches equilibrium, at which point the net force becomes zero.
When the sphere is dropped into the medium, two main forces act on it: the gravitational force (weight) acting downwards and the buoyant force acting upwards.
The gravitational force (weight) acting on the sphere can be expressed as:
Fg=mg
where m is the mass of the sphere and g is the acceleration due to gravity.
The buoyant force (Fb) acting on the sphere can be calculated using Archimedes' principle, which states that the buoyant force is equal to the weight of the fluid displaced by the sphere. It can be expressed as:
Fb=ρVg
where ρ is the density of the medium, V is the volume of the sphere, and g is the acceleration due to gravity.
As the sphere falls, the net force (Fnet) acting on it can be expressed as:
Fnet=Fg−Fb
Initially, when the sphere is dropped, the buoyant force is less than the gravitational force, resulting in a downward acceleration.
As the sphere continues to fall, it displaces more fluid, which increases the buoyant force. Eventually, the buoyant force will increase to equal the gravitational force. At this point, the sphere reaches a state of equilibrium, and the net force becomes zero:
Fg=Fb
This means that the sphere will stop accelerating and will fall at a constant velocity, known as terminal velocity.
Thus, the force acting downwards on the sphere decreases as it falls due to the increasing buoyant force until it reaches equilibrium.
The force acting downwards on the sphere decreases until it reaches equilibrium, at which point the net force becomes zero.
Topper's Solved these Questions
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Exercise- 2 PART - I
Explore 9 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Exercise- 2 PART - II
Explore 6 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Exercise- 1 PART - I
Explore 8 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 92 illustration
Explore 2 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercise
Explore 43 Videos
Similar Questions
Knowledge Check
An aluminium sphere is dipped into water at 10∘C. If the water is now heated, the force of buoyancy on the sphere
Awill remain the sameBwill increaseCwill decreaseDmay increase or decrease depending on the initial volume of sphere
A sphere of mass m rolls without slipping on an inclined plane of inclination θ. Find the linear acceleration of the sphere and the force of friction acting on it. What should be the minimum coefficient of static friction to support pure rolling?
View SolutionDefine terminal velocity: A steel ball is dropped in a viscous oil. Draw a simple labelled diagram to show the forces acting on the ball as it falls through the oil.
View SolutionA ball is kept at a height h above the surface of a heavy transparent sphere made of a material of refractive index The radius of the sphere is R. At t = 0, the ball is dropped to fall normally on the sphere. Find the speed of the image formed as a function of time for t<√2hg. Consider only the image by a single refraction.
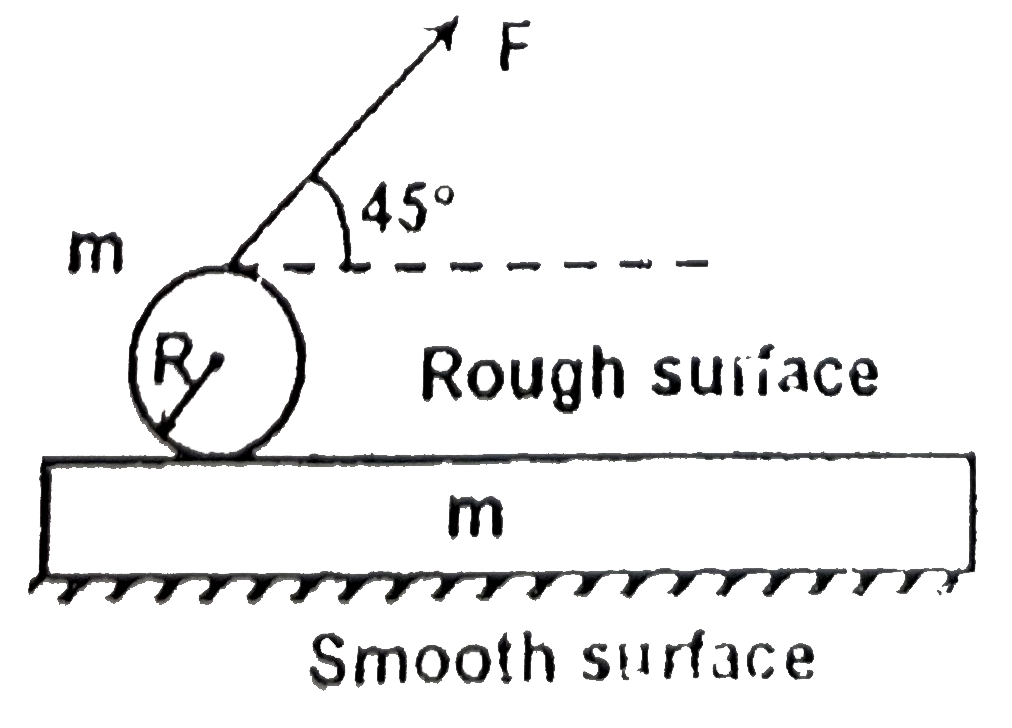
View SolutionA plank of mass m is placed on a smooth surface. Now, a uniform solid sphere of equal mass m and radius R is placed on the plank as shown in the figure. A force F is applied at topmost point of the sphere at an angle of 45∘ to the horizontal. Surface between the plank and the sphere is extremely rough so that there is no slip between the plank and the sphere. The force of firction acting between the plank and the sphere is Fk√2. Find the value of k.
View SolutionA sphere is dropped into a viscous liquid of viscosity η from some height if the density of material and liquid are ρ and σ respectively (ρ>σ) then which of the following is/are incorrect.
(a). The acceleration of the sphere just after entering the liquid is g(ρ−σρ)
(b). Time taken to attain terminal speed t∝ρ0
(C)AT TERMINAL SPEED VISCOUS FORCE IS MAXIMUM (d). At terminal speed, the net force acting on the sphere is zero.
View SolutionA sphere of density ρ is half submerged in a liquid of density σ and surface tension T. The sphere remains in equilibrium. Find radius of the sphere (assume the force due to surface tension acts tangentially to surface of sphere)
View SolutionA disc and a solid sphere of same mass and radius roll down an inclined plane. The ratio of thhe friction force acting on the disc and sphere is
View Solution


