A rectagular wire frame with one movable side is convered by a soap film (fig.). What force should be applied to the movable side to counterbalance it ? What work will be done if this side of the frame is moved a distance S=2cm ? The length of the movable side is l=6cm. The surface tension of the soap film is α=40dyne/cm.
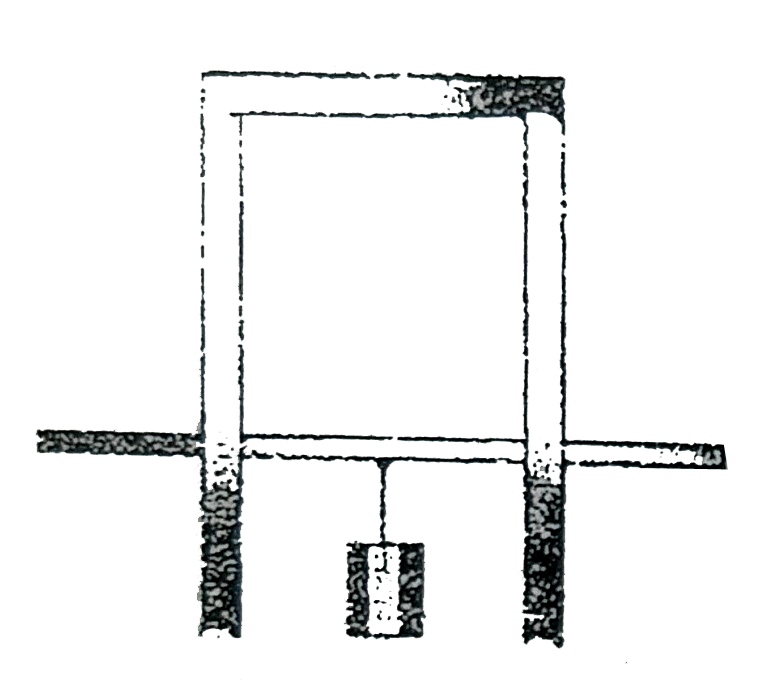
The correct Answer is:F=480dyn,w=960erg
Pexcess=4TR=4×2.5×10−25×10−3=20N/m2
p=patm+hρg+2Tr=1.01×105+.40×1.2×103×9.8+2×2.5×10−25×10−3=1.05714×105N/m2
Topper's Solved these Questions
- SURFACE TENSIONBook:RESONANCE ENGLISHChapter:SURFACE TENSIONExercise:Exercise- 3 PART - II
Explore 7 Videos
- STRING WAVESBook:RESONANCE ENGLISHChapter:STRING WAVESExercise:Exercise
Explore 32 Videos
- UNITS, DIMENSION & MEASUREMENTBook:RESONANCE ENGLISHChapter:UNITS, DIMENSION & MEASUREMENTExercise:Exercise
Explore 27 Videos
Similar Questions
A U-shaped wire is dipped in a soap solution, and removed. A thin soap film formed between the wire and a light slider supports a weight of 1.5×10−2N (which includes the small weigh of the slider). The length of the slider is 30cm. What is the surface tension of the film?
View SolutionIf 72×10−5 J of work is done to increase the radius of a soap bubble from 2 cm to 3 cm. What is the surface tension of the soap solution?
View Solution
Knowledge Check
The work done is increasing the size of a soap film from 10 cm × 6 cm to 10 cm × 11 cm is 3×10−4 joule. The surface tension of the film is
A1.5×10−2 N/mB3.0×10−2 N/mC6.0×10−2 N/mD11.0×10−2 N/mThe work done in increasing the size of a rectangular soap film with dimensions 8 cm x 3.75 cm to 10 cm x 6 cm is 2×10−4J. The surface tension of the film in (Nm−1) is
A1.65×10−2B3.3×10−2C6.6×10−2D8.25×10−2A particle is executing simple harmonic motion of amplitude 5 cm and period 6 s. How long will it take to move from one end of its path on one side of mean position to a position 2.5 cm on the same side of the mean position ?
A1 sB1.5 sC3 sD3.5 s
There is a soap film on a rectangular frame of wire of area 4×4cm2 . If the area of the frame is increased to 4×5cm2,find the work done in the process. Given surface tension of soap films =3×10−2Nm−1.
View SolutionVolume of a cube is increasing at the rate of 9cm3/s if the length of its side is equal to 10 cm than at what rate its surface area is increasing?
View SolutionA soap film is on a rectangular wire ring of size 2 cm × 3 cm. If the size of the film is changed to 3 cm × 3 cm, calculate the work done in this process. (The surface tension of soap solution is 3.0×10−2Nm−1).
View Solution2. The lid of a rectangular box of sides 40 cm by 10 cm is sealed all round with tape. What is the length of the tape required?
View SolutionA film of soap solution is formed on a loop frame loop of 6.28cm long thread is gently put on the film and the film is broken with a needle inside the loop. The tread loop takes the shape of a circle. Find the tension in the thread. Surface tension of soap solution =0.030n/m.
View Solution

