Which of these is/are representing electrostatic field? (x and y are space coordinates)
yˆi+xˆj
sinxˆi
xˆi+yˆj
x2ˆi+yˆj
The correct Answer is:A, C, D
To determine which of the given fields represent electrostatic fields, we need to apply the condition for an electrostatic field. The condition states that for a field represented as E=Ex^i+Ey^j, the following must hold true:
∂Ex∂y=∂Ey∂x
We will analyze each option step by step.
Step 1: Analyze Option A
Given field: E=y^i+x^j
- Ex=y
- Ey=x
Now, calculate the derivatives:
- ∂Ex∂y=∂y∂y=1
- ∂Ey∂x=∂x∂x=1
Since both derivatives are equal:
∂Ex∂y=∂Ey∂x⇒1=1
Conclusion: Option A represents an electrostatic field.
Step 2: Analyze Option B
Given field: E=sin(x)^i+0^j
- Ex=sin(x)
- Ey=0
Now, calculate the derivatives:
- ∂Ex∂y=∂sin(x)∂y=0
- ∂Ey∂x=∂0∂x=0
Since both derivatives are equal:
∂Ex∂y=∂Ey∂x⇒0=0
Conclusion: Option B represents an electrostatic field.
Step 3: Analyze Option C
Given field: E=x^i+y^j
- Ex=x
- Ey=y
Now, calculate the derivatives:
- ∂Ex∂y=∂x∂y=0
- ∂Ey∂x=∂y∂x=0
Since both derivatives are equal:
∂Ex∂y=∂Ey∂x⇒0=0
Conclusion: Option C represents an electrostatic field.
Step 4: Analyze Option D
Given field: E=x2^i+y^j
- Ex=x2
- Ey=y
Now, calculate the derivatives:
- ∂Ex∂y=∂x2∂y=0
- ∂Ey∂x=∂y∂x=0
Since both derivatives are equal:
∂Ex∂y=∂Ey∂x⇒0=0
Conclusion: Option D represents an electrostatic field.
Final Conclusion
All four options A, B, C, and D represent electrostatic fields.
---
Given field: E=y^i+x^j
- Ey=x
- ∂Ex∂y=∂y∂y=1
- ∂Ey∂x=∂x∂x=1
∂Ex∂y=∂Ey∂x⇒1=1
Conclusion: Option A represents an electrostatic field.
Given field: E=sin(x)^i+0^j
- Ey=0
- ∂Ex∂y=∂sin(x)∂y=0
- ∂Ey∂x=∂0∂x=0
∂Ex∂y=∂Ey∂x⇒0=0
Conclusion: Option B represents an electrostatic field.
Given field: E=x^i+y^j
- Ey=y
- ∂Ex∂y=∂x∂y=0
- ∂Ey∂x=∂y∂x=0
∂Ex∂y=∂Ey∂x⇒0=0
Conclusion: Option C represents an electrostatic field.
Given field: E=x2^i+y^j
- Ey=y
- ∂Ex∂y=∂x2∂y=0
- ∂Ey∂x=∂y∂x=0
∂Ex∂y=∂Ey∂x⇒0=0
Conclusion: Option D represents an electrostatic field.
All four options A, B, C, and D represent electrostatic fields.
Topper's Solved these Questions
Similar Questions
Knowledge Check
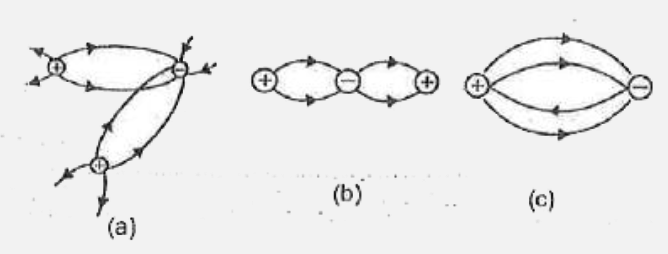
Which of the following curves represent electrostatic field lines correctly?
A B
B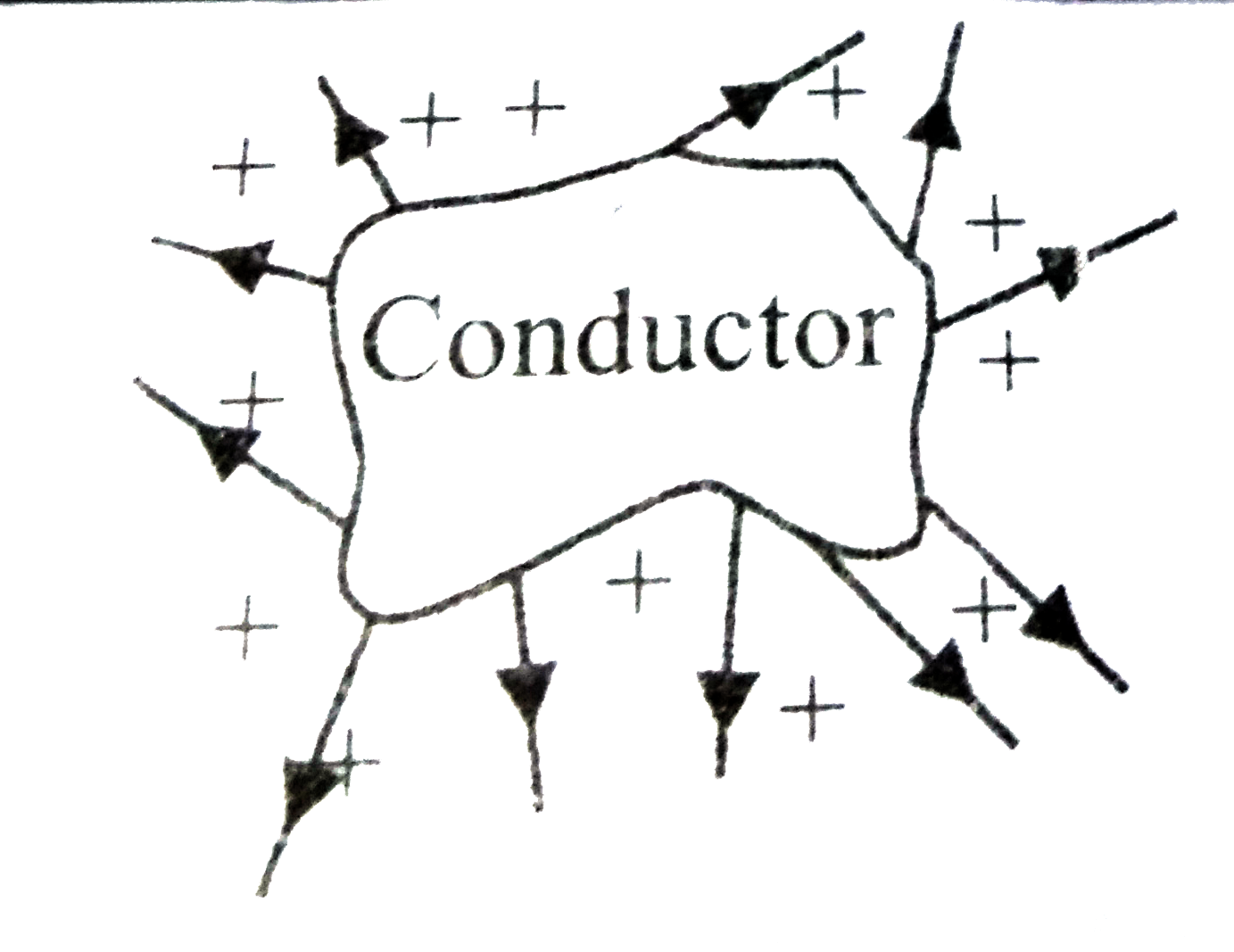 C
C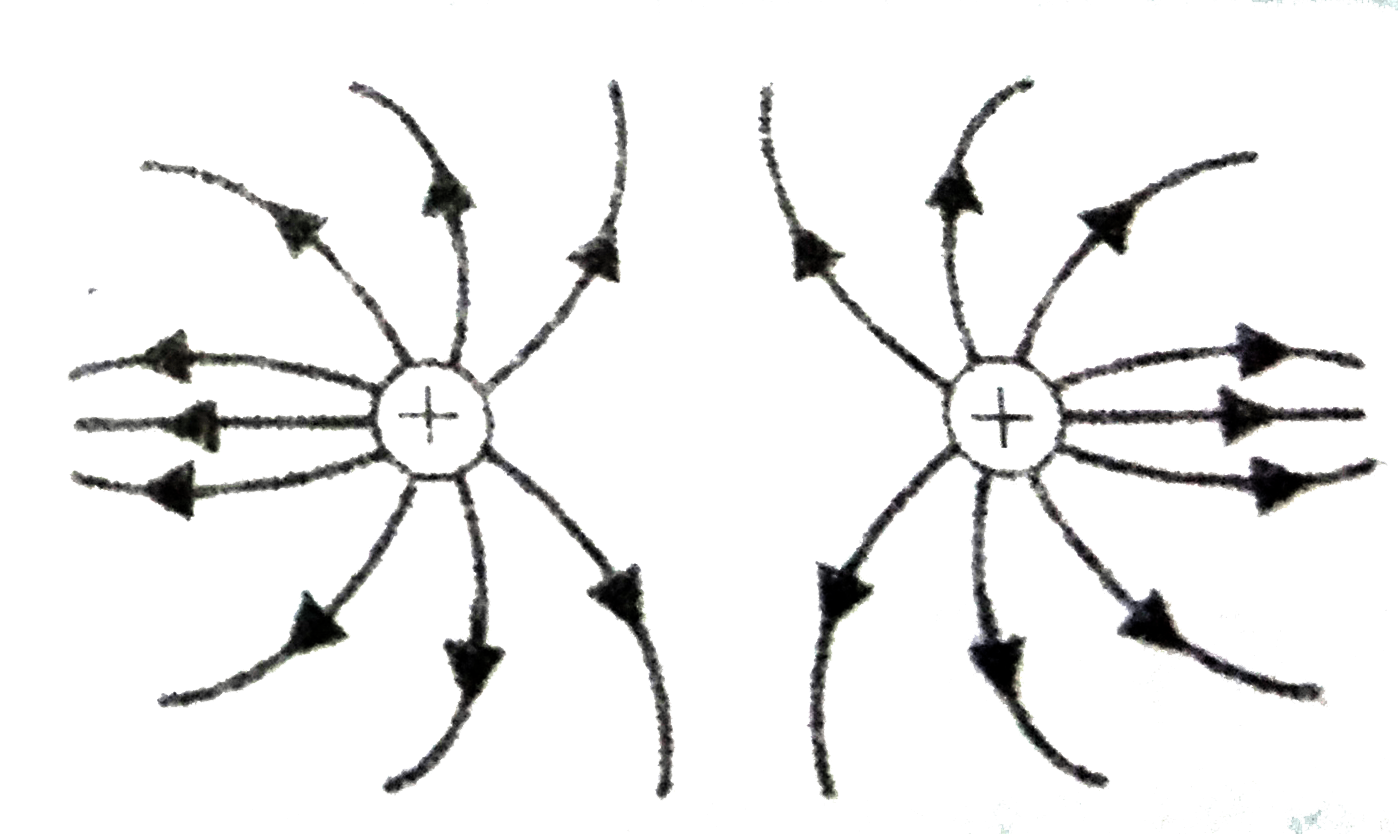 D
D
Why do the electrostatic field lines not form closed loop?
View SolutionWhy do the electrostatic field lines not form closed loops ?
View SolutionWhich of the following curves shown below cannot possibly represent electrostatic field lines?
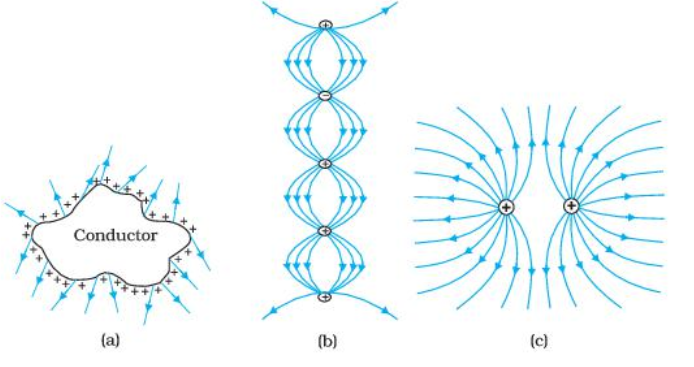
View SolutionWhich of the following field lines pattern could represent a magnetic field?
View SolutionMatch the column
Column IColumn II(A)A stationary positive charge(p)Exert electrostatic force on other charge directly(B)A stationary negative charge(q)Produces electrostatic field directly(C)A stationary electrically neutrally object(r)Acceleration in the direction of electrostatic field(D)Electrostatic field(s)Accelerates opposite to the direction of electrostatic field(t)Cannot exert force on itself
View SolutionWhich of the following may represent the curve x = 2y+ 3?
View SolutionConsider the three statements in context of electrostatic field lines.
STATEMENT-1 : Electrostatic field lines are continuous curves in space.
STATEMENTS-2 : Electrostatic field lines are always perpendicular to equipotential surface.
STATEMENT-3 : A charge when released in electrostatic field moves along electrostatic field lines.
View Solution