Let f(x) be real valued continuous function on R defined as f(x)=x2e−|x| then
f(x) is increasing in
e24<k<∞
e22
0<k≤4e2
e24
The correct Answer is:A, D
Graph of f(x) 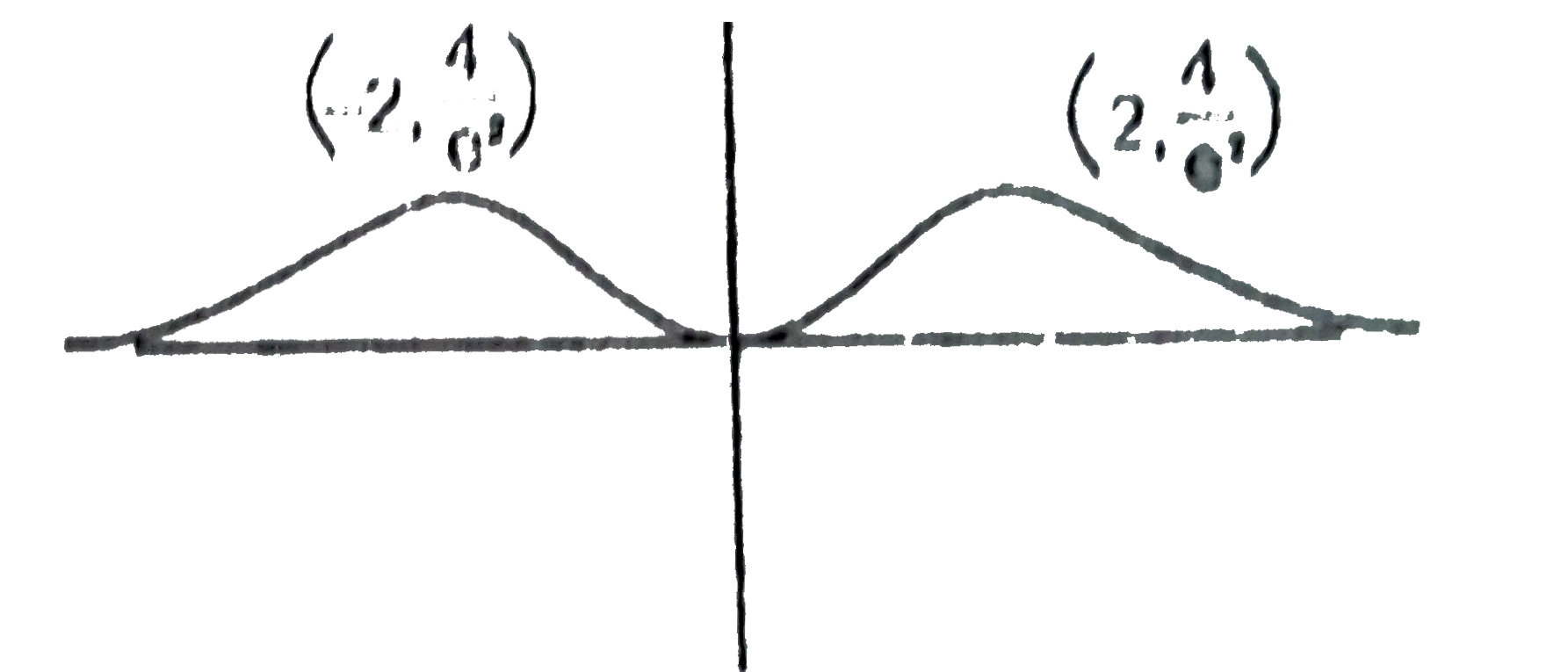
y=kx2 will intersect y=e|x|
Then kx2=e|x|
x2e|x|=1k⇒1k=4e2⇒k=e24
Topper's Solved these Questions
Similar Questions
Let f(x)be real valued continous funcion on R defined as f(x) =x2e−|x|
Number of points of inflection for y=f(x) is (a) 1 (b) 2 (c) 3 (d) 4View SolutionLet f be a real valued function defined by f(x)=ex−e−|x|ex+e|x| , then the range of f(x) is: (a)R (b) [0,1] (c) [0,1) (d) [0,12)
View SolutionLet f be a real-valued function defined by f(x)=3x2+2x+5 Find f'(1).
View SolutionIf f(x) is a real-valued function defined as f(x)=In(1−sinx), then the graph of f(x) is
View SolutionLet f be a real valued function defined by f(x)=x2+1. Find f'(2).
View SolutionLet f:R→R be a functino defined by f(x)=ex−e−x,thenf−1(x)=
View SolutionIf f:R→R be a function defined as f(x)=x2−8x2+2, then f is
View SolutionLet be a real valued function defined by f(x)=e+ex, then the range of f(x) is :
View SolutionLet f:R→R be a function defined as f(x)=x2−6x2+2, then f is
View SolutionLet f(x) be a continuous function such that f(0)=1andf(x)=f(x7)=x7∀x∈R, then f(42) is
View Solution
