Freezing point lowering expression is
ΔTf=Kfm (molality)
Which of the following assumptions are considered for the validity of above equation ?
The solution is dilute
The ΔHf (latent heat of fusion of solvent) is independent of temperature between the actual and normal freezing point.
The solid-phase consists of pure solvent when solution is allowed to cool
ΔTf is not equal to 3Kf for 3mol:−1 solution
To solve the question regarding the assumptions for the validity of the freezing point lowering expression ΔTf=Kf⋅m, we can break it down into a step-by-step explanation.
1. Understanding the Equation:
The equation ΔTf=Kf⋅m relates the change in freezing point (ΔTf) to the molality (m) of the solution and the freezing point depression constant (Kf) of the solvent.
2. Assumption of Dilute Solutions:
The equation is valid primarily for dilute solutions. This means that the concentration of the solute should be low enough that the interactions between solute particles do not significantly affect the properties of the solvent.
3. Independence of ΔHf from Temperature:
The enthalpy of fusion (ΔHf) of the solvent should be independent of temperature between the actual freezing point and the normal freezing point. This ensures that the freezing point depression is consistent across the temperature range.
4. Solid Phase Consisting of Pure Solvent:
When the solution is allowed to cool, the solid phase that forms should consist of pure solvent. This means that the solute does not crystallize out with the solvent, which would alter the freezing point depression.
5. Limitation on Concentration:
The equation does not hold true for very concentrated solutions. For example, ΔTf is not equal to 3Kf for a 3 molal solution. This indicates that the linear relationship breaks down at higher concentrations.
6. Intermolecular Forces:
The intermolecular forces between solvent molecules are involved in the freezing point depression. The enthalpy change of the solution is almost identical to that of the solvent, which is a crucial assumption for the validity of the equation.
Conclusion:
Based on these assumptions, the correct option that reflects the assumptions for the validity of the freezing point lowering equation is option number B.
The equation ΔTf=Kf⋅m relates the change in freezing point (ΔTf) to the molality (m) of the solution and the freezing point depression constant (Kf) of the solvent.
The equation is valid primarily for dilute solutions. This means that the concentration of the solute should be low enough that the interactions between solute particles do not significantly affect the properties of the solvent.
The enthalpy of fusion (ΔHf) of the solvent should be independent of temperature between the actual freezing point and the normal freezing point. This ensures that the freezing point depression is consistent across the temperature range.
When the solution is allowed to cool, the solid phase that forms should consist of pure solvent. This means that the solute does not crystallize out with the solvent, which would alter the freezing point depression.
The equation does not hold true for very concentrated solutions. For example, ΔTf is not equal to 3Kf for a 3 molal solution. This indicates that the linear relationship breaks down at higher concentrations.
The intermolecular forces between solvent molecules are involved in the freezing point depression. The enthalpy change of the solution is almost identical to that of the solvent, which is a crucial assumption for the validity of the equation.
Based on these assumptions, the correct option that reflects the assumptions for the validity of the freezing point lowering equation is option number B.
Topper's Solved these Questions
- SOLUTIONSBOOK - RESONANCE ENGLISHCHAPTER - SOLUTIONSEXERCISE - Advabced Level Problems (PART-2)
35 Videos
- SOLUTIONSBOOK - RESONANCE ENGLISHCHAPTER - SOLUTIONSEXERCISE - EXERCISE-3(PART-3)
30 Videos
- SOLUTION AND COLLIGATIVE PROPERTIESBOOK - RESONANCE ENGLISHCHAPTER - SOLUTION AND COLLIGATIVE PROPERTIESEXERCISE - PHYSICAL CHEMITRY (SOLUTION & COLLIGATIVE PROPERTIES)
52 Videos
- STEREOISOMERISMBOOK - RESONANCE ENGLISHCHAPTER - STEREOISOMERISMEXERCISE - EXERCISE (PART III : PRACTICE TEST-2 (IIT-JEE (ADVANCED PATTERN))
23 Videos
Similar Questions
Which of the following exhibits the greatest freezing point lowering per mole of solute ?
View SolutionA system of greater disorder of molecules is more probable. The disorder of molecules is reflected by the entropy of the system. A liquid vapourizes to form a more disordered gas. When a solute is present, there is additional contribution to the entropy of the liquid due to increased randomness. As the entropy of solution is higher than that of pure liquid, there is weaker tendency to form the gas. Thus, a solute (non-volatile) lowers the vapour pressure of a liquid, and hence a higher boiling point of the solution.
Similarly, the greater randomness of the solution opposes the tendercy to freeze. In consequence, a lower temperature must be reached for achieving the equilibrium between the solid (frozen solvent) and the solution. The elevation in boiling point (ΔTb) and depression in freezing point (ΔTf) of a solution are the colligative properties which depend only on the concentration of particles of the solute and not their identity. For dilute solutions, (ΔTb) and (ΔTf) are proportional to the molarity of the solute in the solution.
Dissolution of a non-volatile solute into a liquid leads to
View Solution
Knowledge Check
In the equation above, k is a constant. For which of the following values f k does the equation have at least one re3al solution ?
A2B3C4D5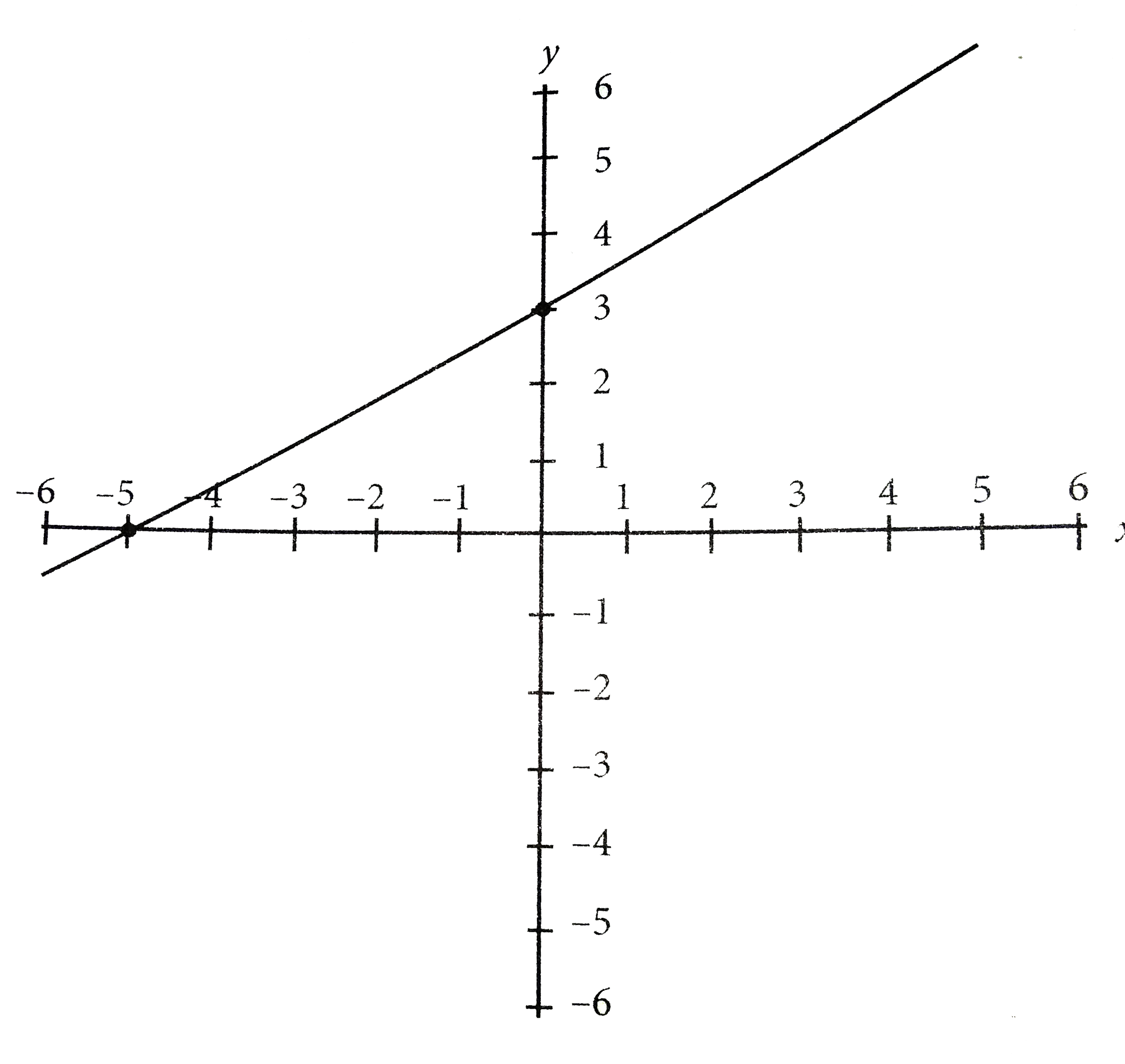
In the figure above, of y=f(x) is shown. Which of the following could be the equation of f(x)?Af(x)=−35x+3Bf(x)=−35x−3Cf(x)=35x−3Df(x)=35x+3
The table above shows a few values of the linear function f. which of the following equations defines f?Af(x)=2x−3Bf(x)=−2x+3Cf(x)=−3x+2Df(x)=3x−2
A system of greater disorder of molecules is more probable. The disorder of molecules is reflected by the entropy of the system. A liquid vapourizes to form a more disordered gas. When a solute is present, there is additional contribution to the entropy of the liquid due to increased randomness. As the entropy of solution is higher than that of pure liquid, there is weaker tendency to form the gas. Thus, a solute (non-volatile) lowers the vapour pressure of a liquid, and hence a higher boiling point of the solution.
Similarly, the greater randomness of the solution opposes the tendercy to freeze. In consequence, a lower temperature must be reached for achieving the equilibrium between the solid (frozen solvent) and the solution. The elevation in boiling point (ΔTb) and depression in freezing point (ΔTf) of a solution are the colligative properties which depend only on the concentration of particles of the solute and not their identity. For dilute solutions, (ΔTb) and (ΔTf) are proportional to the molarity of the solute in the solution.
To aqueous solution of Nal, increasing amounts of solid Hgl2 is added. The vapour pressure of the solution
View SolutionFor 1 molal aqueous solution of the following compounds, which one will show the highest freezing point ?
View SolutionAnswer the following questions :
Why the freezing point depression (ΔTf) of 0.4M NaCl solution is nearly twice than that of 0.4M glucose solution ?
View Solutionwhen some NaCl was dissolved in water, the freezing point depression was nmerically equal to twice the molal f.p. depression constant. The relative lowering of vapour pressure of the solution in nearly :
View SolutionWhy the freezing point depression (ΔTf) of 0.4 M NaCl solution is nearly twice than that of 0.4M glucose solution ?
Among equimolal aqueous solutions of MgCl2,NaCl,FeCl2andC12H22O11, which has high osmotic pressure ? Why ?
View Solution
