In the adjacent figure, a uniform cube of mass m and edge l=2m is lying at rest an a rough horizontal surface. A small ball of mass m hits the cbe at its top edge with horizontal speed v0 and sticks to it. Friction is so large that the cube can rotate about the edge 'O' without sliding. Calculate the minimum value of v0 ( in m/s) so that the cube will topple. Ignore any loss of energy due to friction at the edge O and take √2−1=0.4. 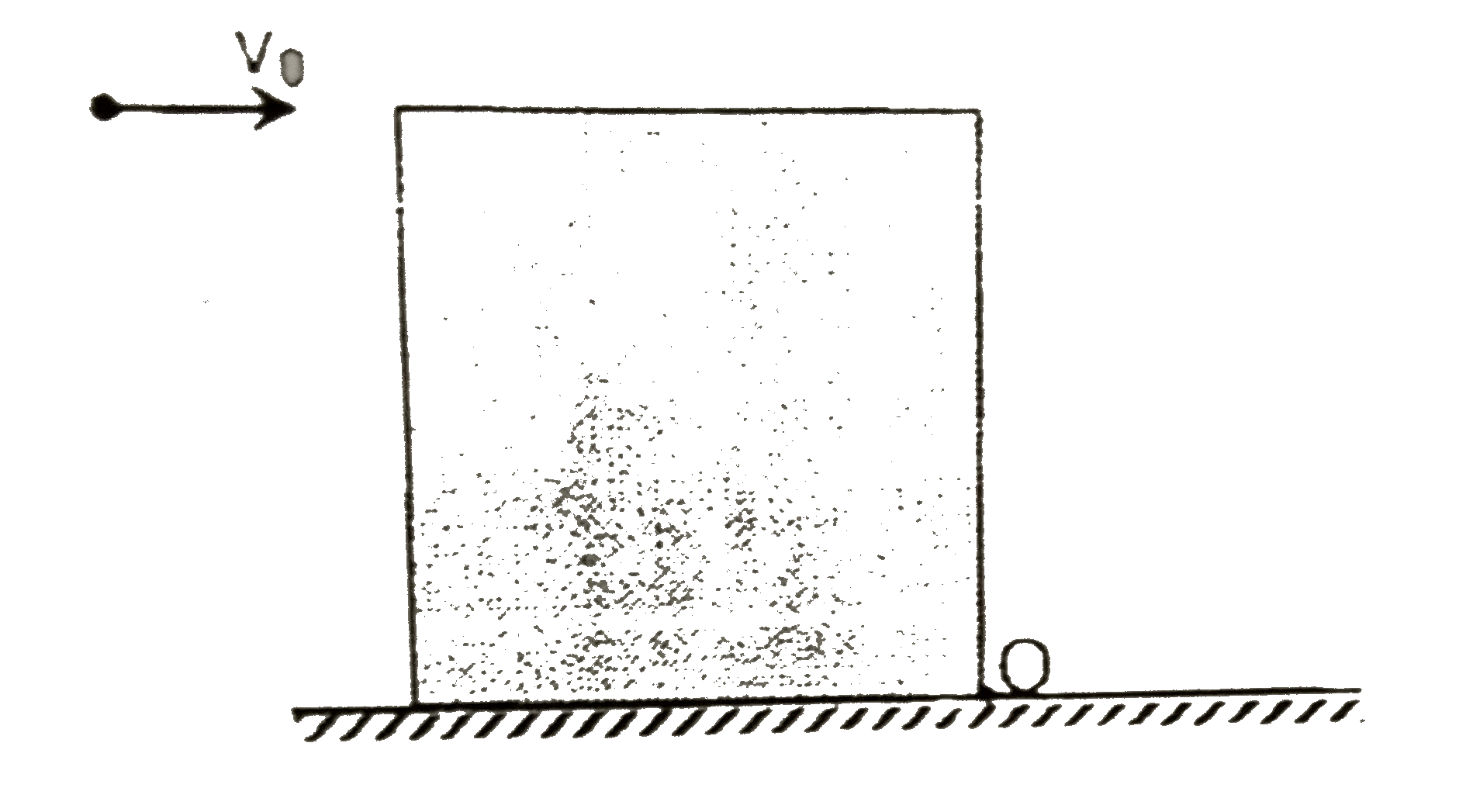
Form COAM
mv0l=8ml23ω
⇒ω=3v08l …(i)
From COE after collision
12×8ml23×ω2
=2mg×3l4×(√2−1) ..(ii)
v0=8ms
Similar Questions
A uniform cube of mass m and edge a moves on a horizontal surface along the positive x-axis, with initial velocity v0. Then
View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

View SolutionThe moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View SolutionA smooth wedge of mass M rests on a smooth horizontal surface. A block of mass m is projected from its lowermost point with velocity v0. What is the maximum height reached by the block?

View SolutionA smooth wedge of mass M rests on a smooth horizontal surface. A block of mass m is projected from its lowermost point with velocity v0. What is the maximum height reached by the block?

View SolutionA small ball of mass m is projected with a minimum horizontal velocity v0 on a smooth wedge of mass M so that it will reach the highest point of the wedge. Find the value of v0

View SolutionThe moment of inertia of a cube of mass m and side a about one of its edges is equal to
View SolutionA wedge shaped block A' of mass M is at rest on a smooth horizontal surface. A small block 'B' of mass 'm' placed at the top edge of inclined plane of length 'l' as shown in the figure. By the time, the block 'B' reaches the bottom end, the wedge A moves a distance of:

View SolutionA unifrom cube of mass m and side a is placed on a frictionless horizontal surface .A vertical force F is applied to the edge as shown in figure ,match the following (most appropriate choice )

View SolutionA uniform cube of side and mass m rests on a rough horizontal surface. A horizontal force F is applied normal to one face at point that is directly above the centre of the face at a height a4 above the centre. The minimum value of F for which the cube begins to topple above an edge without sliding is
View Solution
