A travelling wave travelled in string in +x direction with 2cm/s, particle at x=0 oscillates according to equation y (in mm) =2sin(πt+π/3). What will be the slope of the wave at x=3cm and t=1s ?
−√3π/20
−√3π/2
tan−1(−√3π/2)
−√3π
The correct Answer is:A
Equation of wave can be given as
y=0.2sin(πt−π2x+π3)
slope =∂y∂x=−0.1×πcos(πt−π2x+π3)
∂y∂x=−π10cos[π−3π2+π3]
=−√320
Similar Questions
From a wave equation
y=0.5sin(2π3.2)(64t−x).
the frequency of the wave is
View SolutionA wave is described by the equation y=(1.0mm)sinπ(x2.0cm−t0.01s).
(a) Find time period and wavelength.
(b) Find the speed of particle at x=1.0cm and time t=0.01s.
( c ) What are the speed of the partcle at x=3.0cm, 5.0cmand7.0cm at t=0.01s?
(d) What are the speeds of the partcle at x=1.0cm at t=0.011 , 0.012and0.013s?
View Solution
Knowledge Check
The equation of a wave travelling in a string can be written as y=3cosπ(10t−x). Its wavelength is
A100 cmB2 cmC5 cmDnone of the above
A wave is described by the equation y=(1.0mm)sinπ(x2.0cm−t0.01s).
(a) Find time period and wavelength.
(b) Find the speed of particle at x=1.0cm and time t=0.01s.
( c ) What are the speed of the partcle at x=3.0cm, 5.0cmand7.0cm at t=0.01s?
(d) What are the speeds of the partcle at x=1.0cm at t=0.011 , 0.012and0.013s?
View SolutionA particle moves along the x - axis according to x=A[1+sinωt]. What distance does is travel in time interval from t=0 to t=2.5π/ω ?
View SolutionConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Amplitude of simple harmonic motion of a point on the string that is located at x=1.8cm will be
View SolutionConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
If one end of the string is at x=0 , positions of the nodes can be described as
View SolutionA sinusoidal wave is traveling on a string with speed 40 cm/s. The displacement of the particle of the string at x = 10 cm varies with time according to
y = (5.0cm) sin(1.0−4.0s−1)t)The linear density of the string is 4.0 g/cm
View SolutionA particle is performing SHM according to the equation x=(3cm)sin(2πt18+π6), where t is in seconds. The distance travelled by the particle in 39 s is
View SolutionConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Figure 7.104( c) shows the standing wave pattern at t=0 due to superposition of waves given by y1 and y2 in Figs.7.104(a) and (b) . In Fig. 7.104 (c ) , N is a node and A and antinode . At this instant say t=0 , instantaneous velocity of points on the string named as A
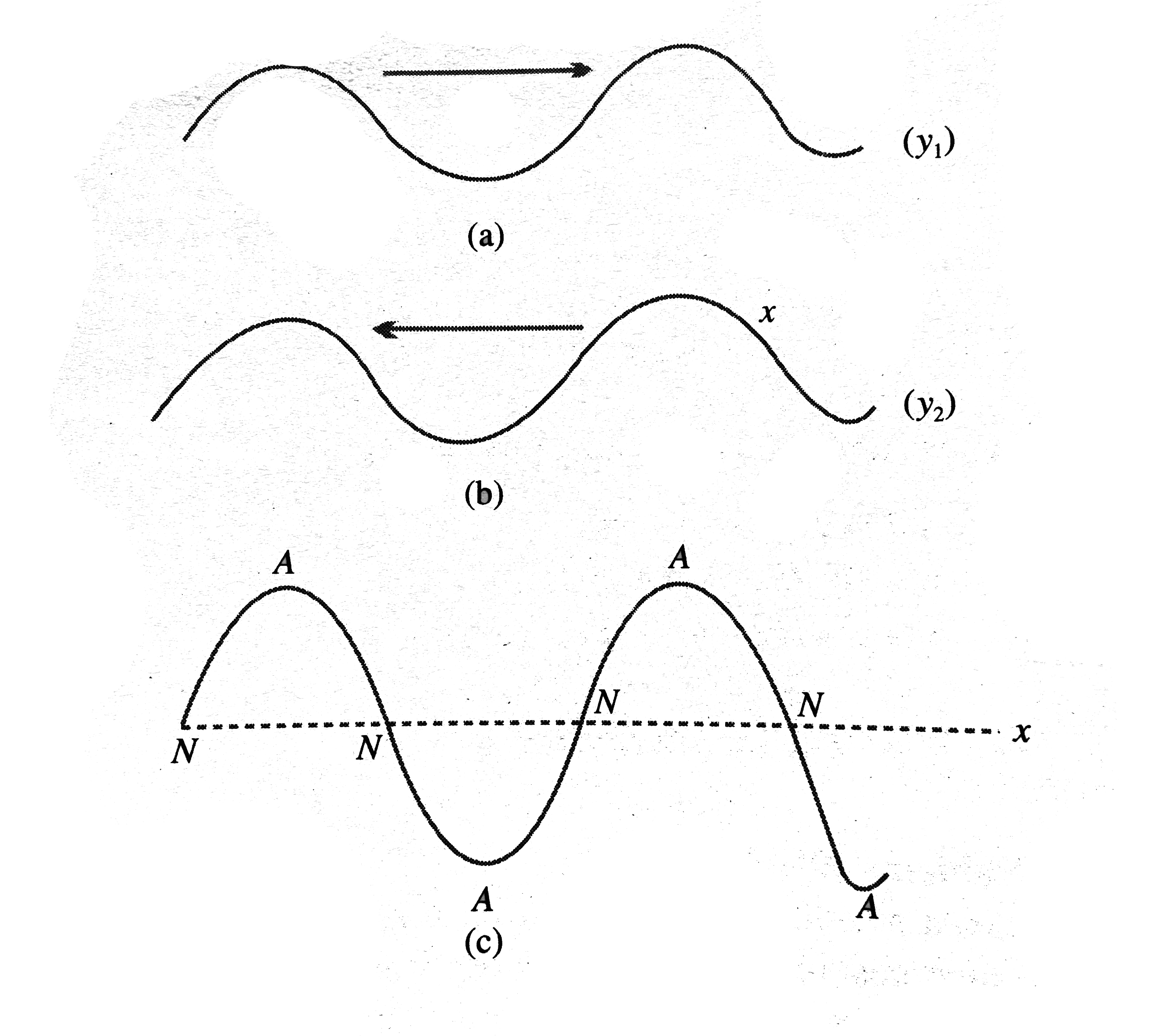
View Solution