A tunnel is dug inside the earth across one of its diameters. Radius of earth is R and its mass is M. A particle is projected inside the tunnel with velocity √2GMR from one of its ends then maximum velocity attained by the particle in the subsequent motion is (assuming tunnel to be frictionless)
A.√GMR
B.√3GMR
C.√2GMR
D.√5GMR
The correct Answer is:B
To solve the problem, we will use the principle of conservation of mechanical energy. The particle is projected into a frictionless tunnel inside the Earth, and we need to find the maximum velocity it attains during its motion.
1. Understanding the Initial Conditions:
- The particle is projected with an initial velocity v0=√2GMR from the surface of the Earth.
2. Potential Energy at the Surface:
- The gravitational potential energy U at the surface of the Earth is given by:
Usurface=−GMmR
- Here, M is the mass of the Earth, m is the mass of the particle, and R is the radius of the Earth.
3. Kinetic Energy at the Surface:
- The kinetic energy K of the particle when projected is:
Ksurface=12mv20=12m(√2GMR)2=12m⋅2GMR=GMmR
4. Total Mechanical Energy at the Surface:
- The total mechanical energy Esurface at the surface is the sum of kinetic and potential energy:
Esurface=Ksurface+Usurface=GMmR−GMmR=0
5. Potential Energy at the Center:
- At the center of the Earth, the potential energy Ucenter is given by:
Ucenter=−32GMmR
6. Kinetic Energy at the Center:
- Let the maximum velocity at the center be vmax. The kinetic energy at the center is:
Kcenter=12mv2max
7. Total Mechanical Energy at the Center:
- The total mechanical energy Ecenter at the center is:
Ecenter=Kcenter+Ucenter=12mv2max−32GMmR
8. Setting Total Energies Equal:
- Since mechanical energy is conserved, we set Esurface=Ecenter:
0=12mv2max−32GMmR
9. Solving for Maximum Velocity:
- Rearranging gives:
12mv2max=32GMmR
- Dividing both sides by m and multiplying by 2:
v2max=3GMR
- Taking the square root:
vmax=√3GMR
Final Answer:
The maximum velocity attained by the particle in the subsequent motion is:
vmax=√3GMR
- The particle is projected with an initial velocity v0=√2GMR from the surface of the Earth.
- The gravitational potential energy U at the surface of the Earth is given by:
Usurface=−GMmR
- Here, M is the mass of the Earth, m is the mass of the particle, and R is the radius of the Earth.
- The kinetic energy K of the particle when projected is:
Ksurface=12mv20=12m(√2GMR)2=12m⋅2GMR=GMmR
- The total mechanical energy Esurface at the surface is the sum of kinetic and potential energy:
Esurface=Ksurface+Usurface=GMmR−GMmR=0
- At the center of the Earth, the potential energy Ucenter is given by:
Ucenter=−32GMmR
- Let the maximum velocity at the center be vmax. The kinetic energy at the center is:
Kcenter=12mv2max
- The total mechanical energy Ecenter at the center is:
Ecenter=Kcenter+Ucenter=12mv2max−32GMmR
- Since mechanical energy is conserved, we set Esurface=Ecenter:
0=12mv2max−32GMmR
- Rearranging gives:
12mv2max=32GMmR
- Dividing both sides by m and multiplying by 2:
v2max=3GMR
- Taking the square root:
vmax=√3GMR
The maximum velocity attained by the particle in the subsequent motion is:
vmax=√3GMR
Similar Questions
A tunnel is dug inside the earth across one of its diameters. Radius of earth is R and its mass is M. A particle is projected inside the tunnel with velocity √2GMR from one of its ends then maximum velocit attained by the particle in the subsequent motion is √nGMR (assuming tunnel to be frictionless). Find n
View SolutionA particle is projected vertically upward with with velocity √23GMR from the surface of Earth. The height attained by it is (G, M, R have usual meanings)
View SolutionA particle is projected from the surface of earth with intial speed of 4 km/s. Find the maximum height attained by the particle. Radius of earth = 6400 km and g=9.8m/s2
View SolutionA particle is thrown vertically upwards. If its velocity is half of the maximum height is 20m/s, then maximum height attained by it is
View SolutionA particle starting from rest undergoes a rectilinear motion with acceleration a. The variation of a with time t is shown below. The maximum velocity attained by the particle during its motion is
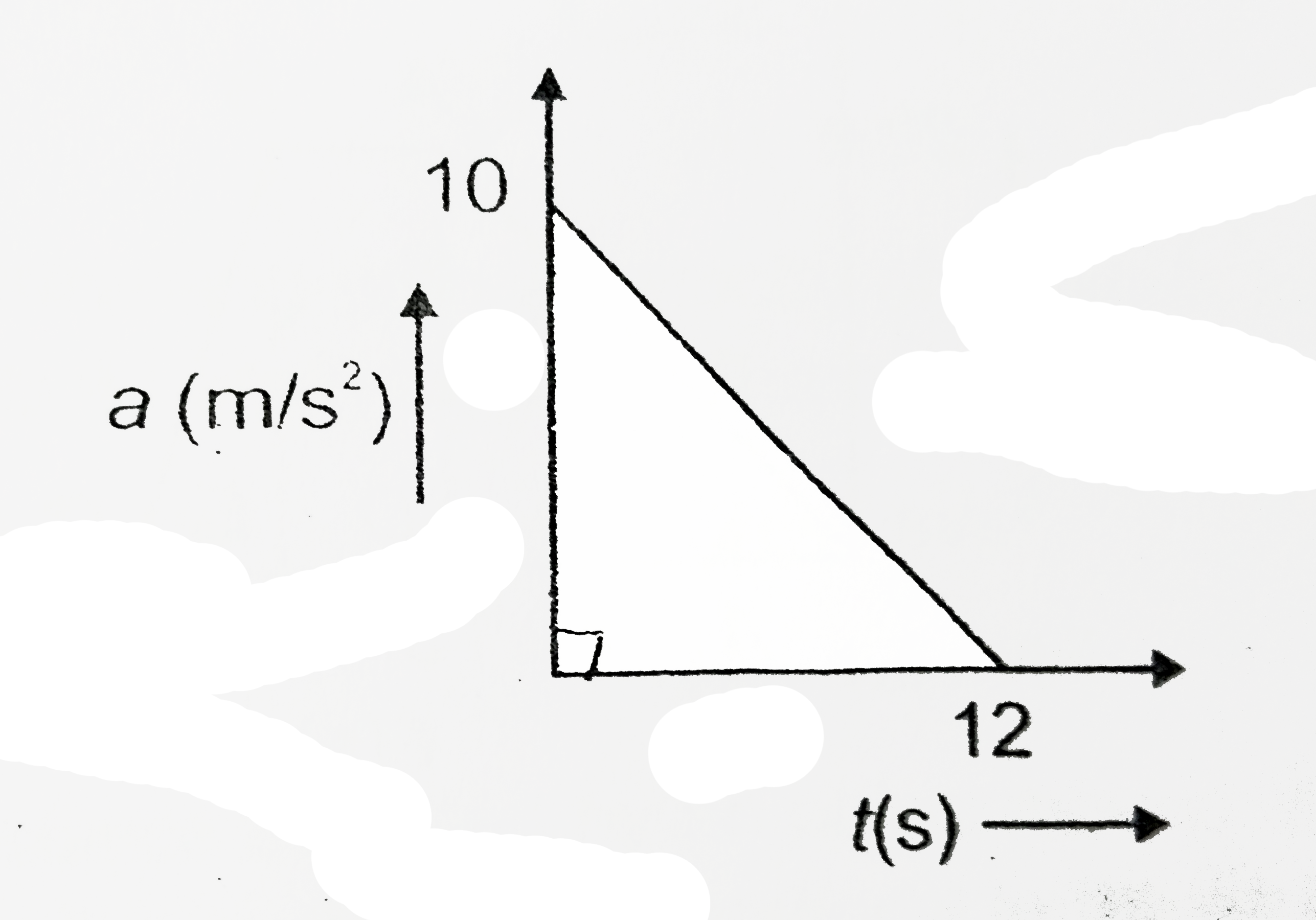
View SolutionWhen a particle is thrown vertically upwards, its velocity at one third of its maximum height is 10√2m/s. The maximum height attained by it is
View SolutionA tunnel is dug across the diameter of earth. A ball is released from the surface of Earth into the tunnel. The velocity of ball when it is at a distance R2 from centre of earth is (where R = radius of Earth and M = mass of Earth)
View SolutionA tunnel is dug in the earth across one of its diameter. Two masses m and 2m are dropped from the two ends of the tunel. The masses collide and stick each other. They perform SHM, the ampulitude of which is (R= radius of earth)
View SolutionA particle of mass m is projected upwards with velocity v=ve2, where ve is the escape velocity then at the maximum height the potential energy of the particle is : (R is radius of earth and M is mass of earth)
View SolutionA body is projected up with a velocity equal to √9GM8R, where M is the mass of the earth and R is the radius of the earth. The maximum distance it reaches from the centre of the earth is
View Solution