Consider a setup of two urea solution of concentration C1 and C2(C2>C1), both at temperature T, separated by a semi permeable membrane. External pressure P1 and P2 respectively are applied on the two solutions. For what values of P1 and P2, osmosis does not occur through the semi permeable membrane? (R= universal gas constant)
P1=C1RT and P2=C2RT
P1= zero and P2=(C2−C1)RT
P1=C2RT and P2=C1RT
P1=2C1RT and P1=(C2+C1)RT
The correct Answer is:A, B, D
To determine the values of external pressures P1 and P2 for which osmosis does not occur through a semi-permeable membrane separating two urea solutions of concentrations C1 and C2 (where C2>C1), we can use the concept of osmotic pressure.
1. Understanding Osmotic Pressure:
- The osmotic pressure (Π) of a solution can be calculated using the formula:
Π=C⋅R⋅T
where C is the concentration of the solution, R is the universal gas constant, and T is the temperature in Kelvin.
2. Setting Up the Conditions:
- We have two solutions:
- Solution 1 with concentration C1 and external pressure P1.
- Solution 2 with concentration C2 and external pressure P2.
- For osmosis to not occur, the external pressures must counterbalance the osmotic pressures of the respective solutions.
3. Equilibrium Condition:
- For no osmosis to occur, the following conditions must be satisfied:
P1=Π1andP2=Π2
where Π1 and Π2 are the osmotic pressures of solutions 1 and 2, respectively.
4. Applying the Osmotic Pressure Formula:
- For Solution 1:
P1=C1⋅R⋅T
- For Solution 2:
P2=C2⋅R⋅T
5. Final Values for Pressures:
- Therefore, the values of P1 and P2 for which osmosis does not occur are:
P1=C1⋅R⋅TandP2=C2⋅R⋅T
Conclusion:
The correct answer is:
- P1=C1⋅R⋅T
- P2=C2⋅R⋅T
- The osmotic pressure (Π) of a solution can be calculated using the formula:
Π=C⋅R⋅T
where C is the concentration of the solution, R is the universal gas constant, and T is the temperature in Kelvin.
- We have two solutions:
- Solution 1 with concentration C1 and external pressure P1.
- Solution 2 with concentration C2 and external pressure P2.
- For osmosis to not occur, the external pressures must counterbalance the osmotic pressures of the respective solutions.
- For no osmosis to occur, the following conditions must be satisfied:
P1=Π1andP2=Π2
where Π1 and Π2 are the osmotic pressures of solutions 1 and 2, respectively.
- For Solution 1:
P1=C1⋅R⋅T
- For Solution 2:
P2=C2⋅R⋅T
- Therefore, the values of P1 and P2 for which osmosis does not occur are:
P1=C1⋅R⋅TandP2=C2⋅R⋅T
The correct answer is:
- P1=C1⋅R⋅T
- P2=C2⋅R⋅T
Similar Questions
V vs T curves at constant pressure P1 and P2 for an ideal gas are shown below
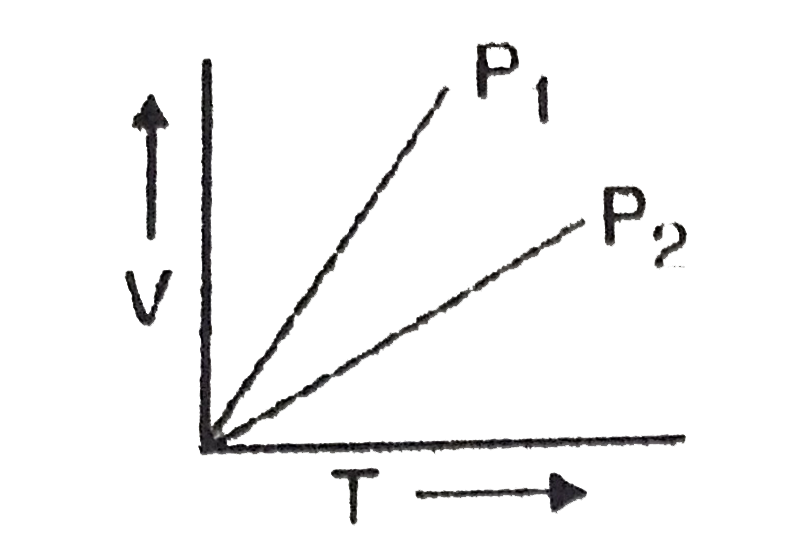
Which is correct ?
View SolutionTwo solutions of KNO3 and CH3COOH are prepared separately. The molarity of both is 0.1M and osmotic pressure is P1 and P2, respectively.
The correct relationship between the osmotic pressure is
View Solution
Knowledge Check
Two cylinder having m1g and m2g of a gas at pressure P1 and P2 respectively are put in cummunication with each other, temperature remaining constant. The common pressure reached will be
AP1P2(m1+m2)P2m1+P1m2BP1P2m1P2m1+P1m2Cm1m2(P1+P2)P2m1(P1+P2)Dm1m2P2P2m1+P1m2
For V versus T curves at constant pressure P1andP2 for an ideal gas are shown in the figure given below
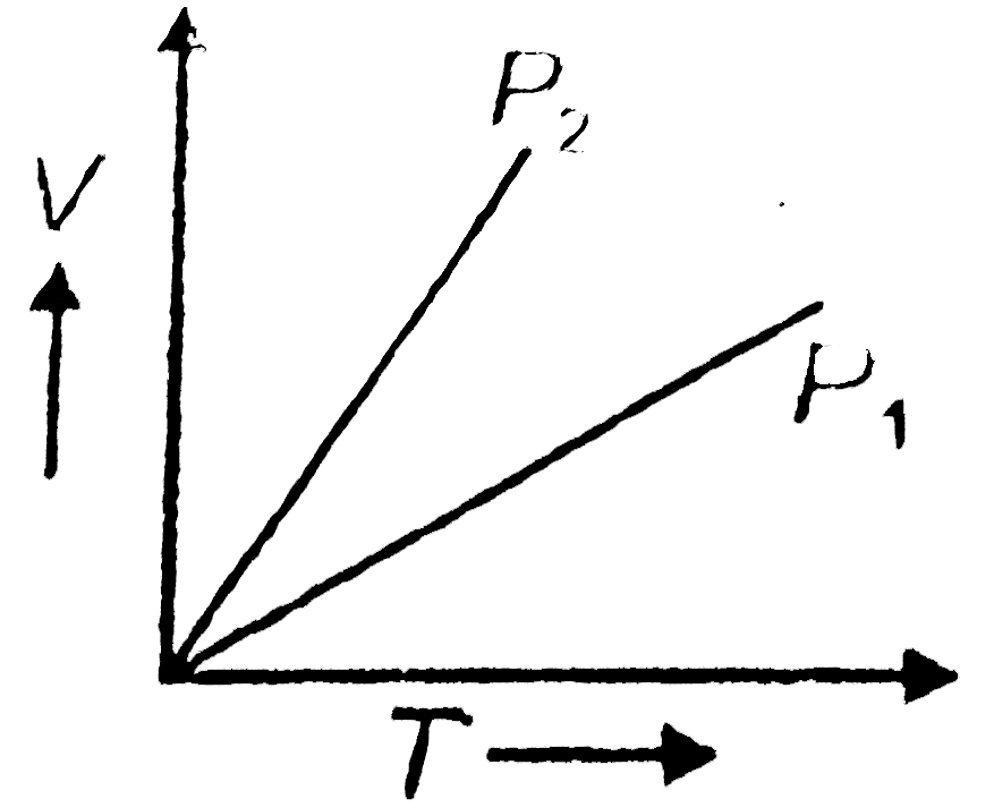
View SolutionIs p = 2 a solution for 2p−1=3?
View SolutionEqual volumes of 0.1 M NaCl and 0.06 M CaCl2 solutions are separated by a semi - permeable membrane in container. For this system, choose the correct answer
View Solution0.1 M NaCl and 0.05 M BaCl2 solutions are separated by a semi-permeable membrane in a container. For this system, choose the correct answer
View SolutionFigure shows volume - temperature (V-T) graph for same mass of an ideal gas at two different pressures P1and P2. Hence
View SolutionFor an ideal gas V−T curves at constant pressure P1 & P2 are shown in figure, from the figure
_E01_061_Q01.png)
View SolutionIf P∘ and Ps are vapour pressure of solvent and its solution, respectively, χ1 and χ2 are mole fractions of solvent and solute, respectively, then
View Solution
