If n1 and n2 are the boundary value principal quantum numbers of a portion fo spectrum of emission spectrum of H atom, determine the wavelength ( in metre ) corresponding to last line ( longest λ) . Given :n1+n2=7,n2−n1=3 and RH=1.097×107m−1 . ( Give your answer in multiple of 10−6)
0.8
0.4
0.1
0.15
The correct Answer is:2
To solve the problem, we need to determine the wavelength corresponding to the last line of the emission spectrum of the hydrogen atom given the conditions on the principal quantum numbers n1 and n2.
1. Identify the equations: We are given two equations based on the principal quantum numbers:
n1+n2=7(1)
n2−n1=3(2)
2. Solve for n1 and n2:
- From equation (1), we can express n2 in terms of n1:
n2=7−n1(3)
- Substitute equation (3) into equation (2):
(7−n1)−n1=3
7−2n1=3
2n1=4⟹n1=2
- Now substitute n1 back into equation (3) to find n2:
n2=7−2=5
3. Use the Rydberg formula: The Rydberg formula for the wavelength (λ) of the emitted light is given by:
1λ=RH(1n21−1n22)
where RH=1.097×107m−1.
4. Substitute the values of n1 and n2:
1λ=1.097×107(122−152)
=1.097×107(14−125)
=1.097×107(25−4100)
=1.097×107(21100)
=1.097×107×0.21
=2.3037×106m−1
5. Calculate λ:
λ=11λ=12.3037×106
λ≈4.344×10−7m
6. Convert to the required format:
λ≈0.4344×10−6m
Rounding to one decimal place gives:
λ≈0.4×10−6m
Final Answer:
Thus, the wavelength corresponding to the last line of the emission spectrum of the hydrogen atom is:
λ≈0.4×10−6m
n1+n2=7(1)
n2−n1=3(2)
- From equation (1), we can express n2 in terms of n1:
n2=7−n1(3)
- Substitute equation (3) into equation (2):
(7−n1)−n1=3
7−2n1=3
2n1=4⟹n1=2
- Now substitute n1 back into equation (3) to find n2:
n2=7−2=5
1λ=RH(1n21−1n22)
where RH=1.097×107m−1.
1λ=1.097×107(122−152)
=1.097×107(14−125)
=1.097×107(25−4100)
=1.097×107(21100)
=1.097×107×0.21
=2.3037×106m−1
λ=11λ=12.3037×106
λ≈4.344×10−7m
λ≈0.4344×10−6m
Rounding to one decimal place gives:
λ≈0.4×10−6m
Thus, the wavelength corresponding to the last line of the emission spectrum of the hydrogen atom is:
λ≈0.4×10−6m
Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - Inorganic chemistry (Chemistry Bonding)
38 Videos
- ATOMIC STRUCTUREBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - ORGANIC CHEMISTRY(Fundamental Concept )
16 Videos
- AROMATIC COMPOUNDS BOOK - RESONANCE ENGLISHCHAPTER - AROMATIC COMPOUNDS EXERCISE - PART-II : JEE (MAIN)
1 Video
- CHEMICAL BONDINGBOOK - RESONANCE ENGLISHCHAPTER - CHEMICAL BONDINGEXERCISE - ORGANIC CHEMISTRY(Fundamental Concept )
6 Videos
Similar Questions
When a transition of electron in He+ takes place from n2 to n1 then wave number in terms of Rydberg constant R will be
(Given n1+n2=4,n2−n1=2)
View Solutioncalculate the longest wavelength in Balmer series and the series limit . (Given R=1.097×107m−1 )
View SolutionThe wavelength of a certain line in the Pashchen series is 1093.6nm. What is the value of nhigh for this line [RH=1.0973×10−7m−1]
View SolutionFind the two longest wavelength (inÅ) emitted when hydrogen atom make transition and the spectrum lines lie in the visible region (R=1.097×107m−1)
View SolutionThe wave number of the first emission line in the Balmer series of H - Spectrum is n36R. The value of 'n' is. (R = Rydberg constant):
View SolutionThe value of n1 for Pashecn series of hydrogen spectrum is(n1= orbit number in which electron falls)
View SolutionGiven below are the spectral lines for an atom of hydrogen. Mark the lines which are not correctly matched with the value of n1 and n2?
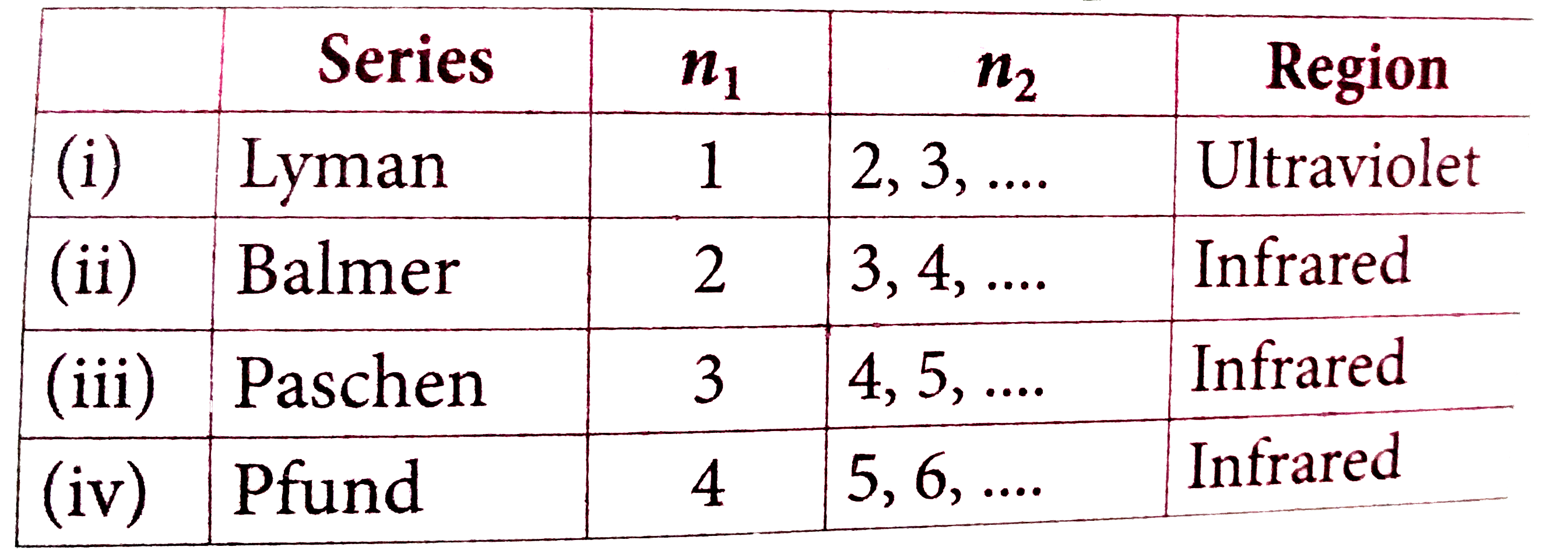
View SolutionWhat are the values of n1 and n2 respectively for HB line in the Lyman series of hydrogen atom spectrum?
View SolutionExcited atoms emit radiations consisting of only certain discrete frequencise or wavelengths. In spectroscopy it is often more convenient to use freuquencies and wave numbers are proportional ot energy and spectroscopy involves transitions between different energy levels . The line spectrum shown by a single electron excited atom (a finger print of an atom) can be given as
1λ=¯vRH.Z2[1n21−1n22]
where Z is atomic number of single electron atom and n1,n2 are integers and if n2>n1, then emission spectrum is noticed and if n2<n1, then absorption spectrum is noticed.
Every line in spectrum can be represented as a difference of two terms RHZ2n21andRHZ2n22.
The ratio of wavelength for II line fo Balmer series and I line of Lyman series for H-like species is :
View SolutionThe value of n1 for Paschen series of hydrogen spectrum is(n1= orbit number in which electron falls)
View Solution
