Sulphur exist in different allotropic forms like and etc. If equal moles of these three forms are taken in separate containers, then the ratio of number of atoms present in them respectively is
The correct Answer is:A
To solve the problem of finding the ratio of the number of atoms present in equal moles of the allotropic forms of sulfur (S₂, S₆, and S₈), we can follow these steps:
Step 1: Understand the allotropic forms of sulfur
Sulfur exists in different molecular forms, specifically S₂, S₆, and S₈. Each of these forms contains a different number of sulfur atoms per molecule.
Step 2: Determine the number of atoms in each form
1. For S₂:
- Each molecule contains 2 sulfur atoms.
- Therefore, 1 mole of S₂ contains 2 atoms×1 mole=2 atoms.
2. For S₆:
- Each molecule contains 6 sulfur atoms.
- Therefore, 1 mole of S₆ contains 6 atoms×1 mole=6 atoms.
3. For S₈:
- Each molecule contains 8 sulfur atoms.
- Therefore, 1 mole of S₈ contains 8 atoms×1 mole=8 atoms.
Step 3: Calculate the ratio of the number of atoms
Now we can express the number of atoms in each form as follows:
- S₂: 2 atoms
- S₆: 6 atoms
- S₈: 8 atoms
The ratio of the number of atoms in S₂, S₆, and S₈ can be written as:
Ratio=2:6:8
Step 4: Simplify the ratio
To simplify the ratio, we can divide each term by the greatest common divisor (GCD), which is 2:
22:62:82=1:3:4
Final Answer
Thus, the ratio of the number of atoms present in the three containers is:
Ratio=1:3:4
Sulfur exists in different molecular forms, specifically S₂, S₆, and S₈. Each of these forms contains a different number of sulfur atoms per molecule.
1. For S₂:
- Each molecule contains 2 sulfur atoms.
- Therefore, 1 mole of S₂ contains 2 atoms×1 mole=2 atoms.
- Each molecule contains 6 sulfur atoms.
- Therefore, 1 mole of S₆ contains 6 atoms×1 mole=6 atoms.
- Each molecule contains 8 sulfur atoms.
- Therefore, 1 mole of S₈ contains 8 atoms×1 mole=8 atoms.
Now we can express the number of atoms in each form as follows:
- S₂: 2 atoms
- S₆: 6 atoms
- S₈: 8 atoms
Ratio=2:6:8
To simplify the ratio, we can divide each term by the greatest common divisor (GCD), which is 2:
22:62:82=1:3:4
Thus, the ratio of the number of atoms present in the three containers is:
Ratio=1:3:4
Topper's Solved these Questions
- MOLE CONCEPTBook:RESONANCE ENGLISHChapter:MOLE CONCEPTExercise:Inorganic chemistry (Periodic Table & Periodicity
Explore 51 Videos
- MOLE CONCEPTBook:RESONANCE ENGLISHChapter:MOLE CONCEPTExercise:ORGANIC CHEMISTRY(BASIC CONCEPTS)
Explore 27 Videos
- IONIC EQUILIBRIUMBook:RESONANCE ENGLISHChapter:IONIC EQUILIBRIUMExercise:ORGANIC CHEMISTRY(Aldehydes , Ketones, Carboxylic acid)
Explore 17 Videos
- ORGANIC REACTION MECHANISMS - IIBook:RESONANCE ENGLISHChapter:ORGANIC REACTION MECHANISMS - IIExercise:APSP Part - 3
Explore 22 Videos
Similar Questions
Knowledge Check
Three different balls of masses m1,m2 and m3 are allowed to roll form rest on three firctionless parth OA, OB and OC respectively from O. The height of O above the ground is h. The respective speeds S1,S2andS3 of m1,m2,andm3 at the bottom A, B and C are
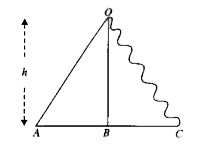 AS1m1S2m2=S3m3Bm1S21=m2S22=m3S32CS2<S1<S3DS1<S2<S3
AS1m1S2m2=S3m3Bm1S21=m2S22=m3S32CS2<S1<S3DS1<S2<S3
The oxidation number of sulphur in S8,S2F2andH2S respectively are:
View SolutionThe oxidation number of sulphur in S8,S2F2,H2SandH2SO4 respectively are :
View SolutionThree moles of B2H6 are completely reacted with methanol. The number of moles of boron containing product formed is.
View SolutionConsider the following representation of oxy-acid, Hn1S2On2, (where S is central sulphur atom annd n1andn2 are natural numbers.) if there are two possible oxy-acid of sulphur A and B contains ratio of n2:n1 are 2 and 4 respectively, then sum of oxidation state of 'S' atom in both oxy-acid will be:
View SolutionThe average oxidation states of sulphur in Na2S2O3andNa2S4O6 are respectively.
View SolutionBoron exist in different allotropic forms. All allotropic form contains icosahedral units (icosahedral is regular shape with 12 corner & 20 faces) with boron atoms at all 12 corners and all bonds are equivalent.
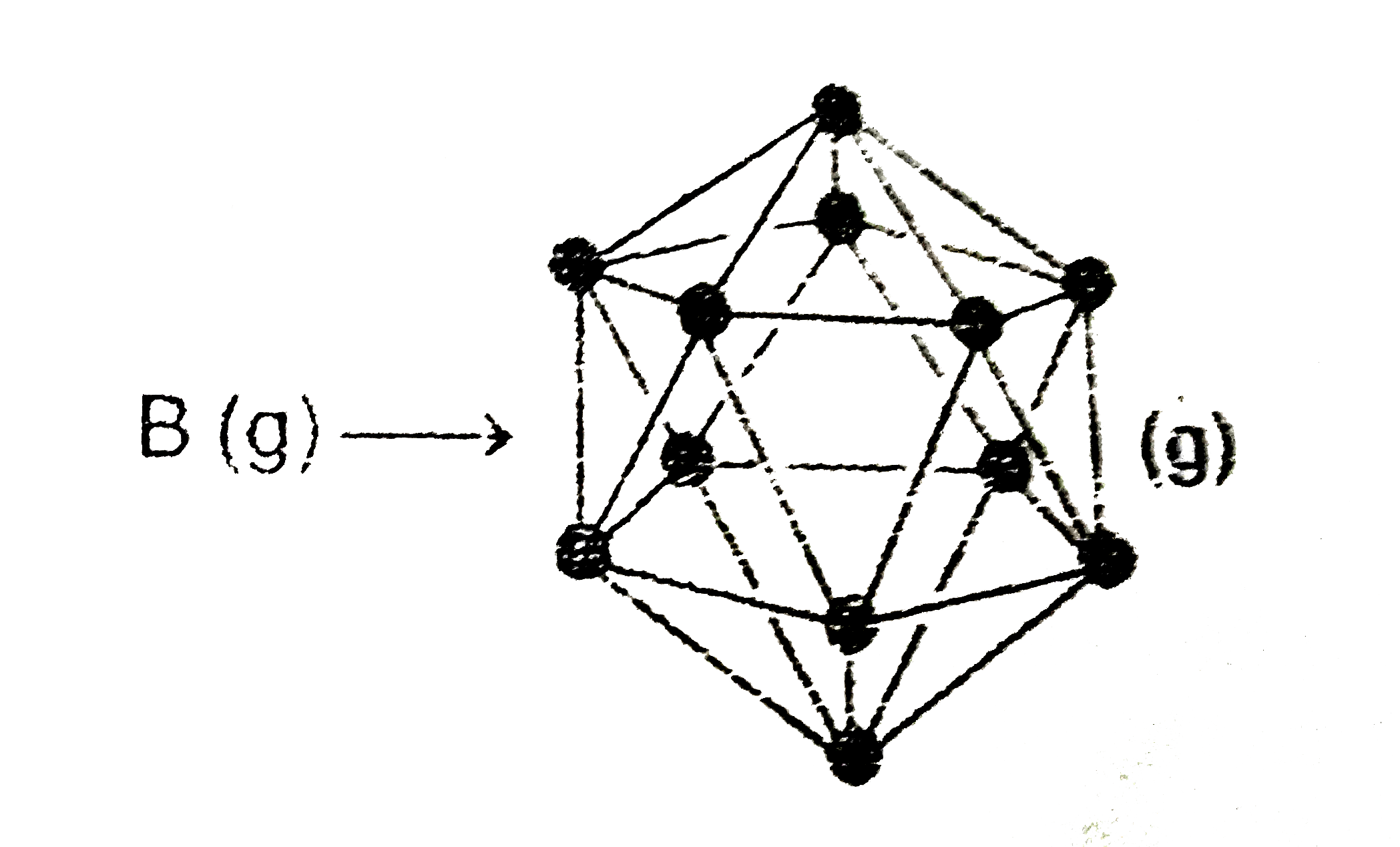
Calculate heat evolved at constant pressure (in KJ) per mole of boron atoms undergoing above change it ΔHBE(B−B)=200KJ/mol. Report you answer after dividing by 100
View SolutionTwo point sources S1 and S2 are 24 cm apart. What should a convex lens of focal length 9 cm be placed between them so that the images of both sources formed at the same place ?
View Solution

