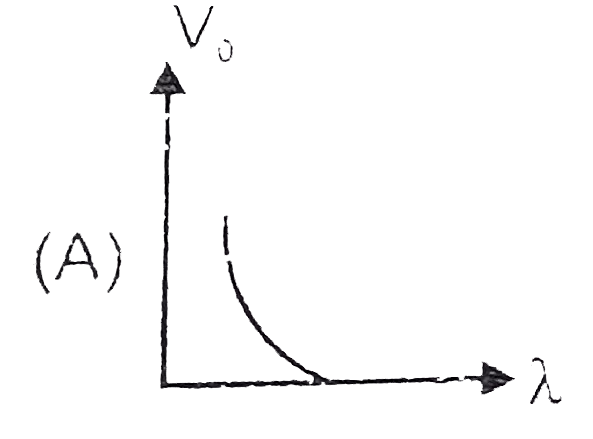
For photo - electric effect with incident photon wavelength λ the stopping is V0 identify the correct variation(s) of V0 with λand1/λ
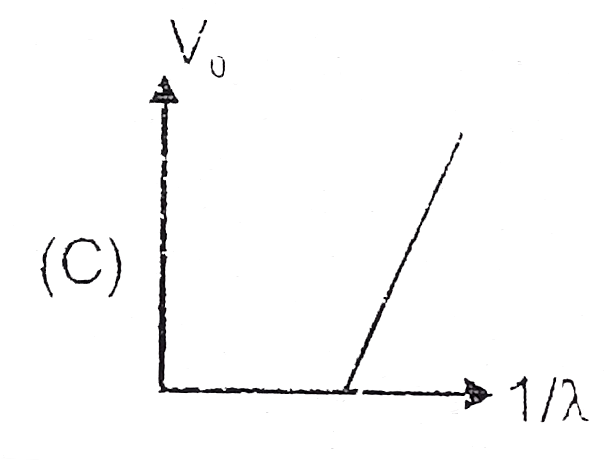
The correct Answer is:A, C
To solve the problem regarding the variation of stopping potential V0 with the wavelength λ and 1λ in the context of the photoelectric effect, we can follow these steps:
Step 1: Understand the Photoelectric Effect Equation
The photoelectric effect is described by the equation:
E=hν=hcλ
where:
- E is the energy of the incident photon,
- h is Planck's constant,
- ν is the frequency of the photon,
- c is the speed of light,
- λ is the wavelength of the incident photon.
The stopping potential V0 is related to the kinetic energy of the emitted electrons and can be expressed as:
eV0=E−ϕ
where:
- e is the charge of the electron,
- ϕ is the work function of the material.
Step 2: Relate Stopping Potential to Wavelength
From the above equations, we can substitute E:
eV0=hcλ−ϕ
Rearranging gives:
V0=hceλ−ϕe
Step 3: Analyze the Equation
In the equation V0=hceλ−ϕe:
- The term hceλ indicates that V0 is inversely proportional to λ.
- The term −ϕe is a constant offset.
Step 4: Variation with λ
As λ increases, the term hceλ decreases, leading to a decrease in V0. Therefore, the variation of V0 with λ is:
- Inverse Relationship: V0 decreases as λ increases.
Step 5: Variation with 1λ
If we express the equation in terms of 1λ:
V0=hce⋅1λ−ϕe
Here, V0 is directly proportional to 1λ:
- Linear Relationship: V0 increases as 1λ increases.
Conclusion
- The variation of stopping potential V0 with λ is inversely proportional.
- The variation of stopping potential V0 with 1λ is directly proportional.
The photoelectric effect is described by the equation:
E=hν=hcλ
where:
- E is the energy of the incident photon,
- h is Planck's constant,
- ν is the frequency of the photon,
- c is the speed of light,
- λ is the wavelength of the incident photon.
eV0=E−ϕ
where:
- e is the charge of the electron,
- ϕ is the work function of the material.
From the above equations, we can substitute E:
eV0=hcλ−ϕ
Rearranging gives:
V0=hceλ−ϕe
In the equation V0=hceλ−ϕe:
- The term hceλ indicates that V0 is inversely proportional to λ.
- The term −ϕe is a constant offset.
As λ increases, the term hceλ decreases, leading to a decrease in V0. Therefore, the variation of V0 with λ is:
- Inverse Relationship: V0 decreases as λ increases.
If we express the equation in terms of 1λ:
V0=hce⋅1λ−ϕe
Here, V0 is directly proportional to 1λ:
- Linear Relationship: V0 increases as 1λ increases.
- The variation of stopping potential V0 with λ is inversely proportional.
- The variation of stopping potential V0 with 1λ is directly proportional.
Topper's Solved these Questions
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems
17 Videos
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Exercise-2 Part-III : Comprehension
12 Videos
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - HIGH LEVEL PROBLEMS
11 Videos
- CAPACITANCEBOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - High Level Problems
16 Videos
Similar Questions
The energy of a photon of wavelength λ is
View SolutionMomentum of a photon of wavelength λ is :
View SolutionThe mass of photon of wavelength λ is given by
View Solutionλ1 and λ2 are used to illuminated the slits. β1 and β2 are the corresponding fringe widths. The wavelength λ1 can produce photoelectric effect when incident on a metal But the wavelength λ2 cannot produce photoelectric effect. The correct relation between β1 and β2 is
View SolutionAn electron and a photon have same wavelength λ, what is ratio of their kinetic energies ?
View SolutionWhen a metallic surface is illuminated with radiation of wavelength λ, the stopping potential is V. If the same surface is illuminated with radiation of wavelength 2λ , the stopping potential is V4. The threshold wavelength surface is :
(a) 5λ (b) 52λ (c) 3λ (d) 4λ
View SolutionWhen a surface 1 cm thick is illuminated with light of wavelength λ, the stopping potential is V0, but when the same surface is illuminated by light of wavelength 3λ, the stopping potential is V06. Find the threshold wavelength for metallic surface.
View SolutionA dye absorbs a photon of wavelength λ and re− emits the same energy into two phorons of wavelengths λ1 and λ2 respectively. The wavelength λ is related with λ1 and λ2 as :
View SolutionWhen a metalic surface is illuminated with light of wavelength λ, the stopping potential is V. the same surface is illuminated by light of wavelength 2λ the stopping potential is V3 The thershold waelength for the surface is
View SolutionWhen a metallic surface is illuminated with monochromatic light of wavelength λ, the stopping potential is 5V0. When the same surface is illuminated with light of wavelength 3λ, the stopping potential is V0. Then the work function of the metallic surface is:
View Solution
