A solid conducting sphere of radius a is enclosed in a concentric shell of radius b>a. The charge on the inner sphere is 3μC and on the conducting shell is −10μC. The potential difference between the conductors is V. If +10μC additional charge is given to the outer shell, the new potential difference is
A. V
B. V/2
C. 2V
D. zero
V
V/2
2V
zero
The correct Answer is:A
To solve the problem step by step, we will analyze the situation involving the solid conducting sphere and the conducting shell.
Step 1: Understand the Configuration
We have a solid conducting sphere of radius a with a charge of +3μC. This sphere is enclosed by a concentric conducting shell of radius b (where b>a), which initially has a charge of −10μC.
Step 2: Determine the Initial Potential Difference
The potential difference V between the inner sphere and the conducting shell can be calculated using the formula:
V=Vinner−Vouter
Where:
- Vinner is the potential at the surface of the inner sphere.
- Vouter is the potential at the inner surface of the conducting shell.
The potential Vinner at the surface of the sphere is given by:
Vinner=Qinner4πϵ0a
Substituting Qinner=3μC:
Vinner=3×10−64πϵ0a
The potential Vouter at the inner surface of the shell can be calculated considering the total charge enclosed by the shell:
Vouter=Qinner+Qshell4πϵ0b
Where Qshell=−10μC:
Vouter=3×10−6−10×10−64πϵ0b=−7×10−64πϵ0b
Thus, the potential difference V is:
V=3×10−64πϵ0a−−7×10−64πϵ0b
Step 3: Adding Additional Charge
Now, we add an additional charge of +10μC to the outer shell. The new charge on the shell becomes:
Qnew shell=−10μC+10μC=0μC
Step 4: Determine the New Potential Difference
With the new charge on the shell being 0μC, the potential at the inner surface of the shell becomes:
Vouter new=3×10−64πϵ0b
Now, the potential difference Vnew becomes:
Vnew=Vinner−Vouter new
Substituting the values:
Vnew=3×10−64πϵ0a−3×10−64πϵ0b
Step 5: Factor Out Common Terms
Factoring out 3×10−64πϵ0:
Vnew=3×10−64πϵ0(1a−1b)
This shows that the new potential difference is still proportional to the original potential difference V.
Conclusion
Since the potential difference depends only on the charges inside and the geometry, and the outer charge does not affect the potential difference, we conclude that the new potential difference remains the same:
Vnew=V
Thus, the correct answer is A. V.
We have a solid conducting sphere of radius a with a charge of +3μC. This sphere is enclosed by a concentric conducting shell of radius b (where b>a), which initially has a charge of −10μC.
The potential difference V between the inner sphere and the conducting shell can be calculated using the formula:
V=Vinner−Vouter
Where:
- Vinner is the potential at the surface of the inner sphere.
- Vouter is the potential at the inner surface of the conducting shell.
Vinner=Qinner4πϵ0a
Substituting Qinner=3μC:
Vinner=3×10−64πϵ0a
Vouter=Qinner+Qshell4πϵ0b
Where Qshell=−10μC:
Vouter=3×10−6−10×10−64πϵ0b=−7×10−64πϵ0b
V=3×10−64πϵ0a−−7×10−64πϵ0b
Now, we add an additional charge of +10μC to the outer shell. The new charge on the shell becomes:
Qnew shell=−10μC+10μC=0μC
With the new charge on the shell being 0μC, the potential at the inner surface of the shell becomes:
Vouter new=3×10−64πϵ0b
Vnew=Vinner−Vouter new
Substituting the values:
Vnew=3×10−64πϵ0a−3×10−64πϵ0b
Factoring out 3×10−64πϵ0:
Vnew=3×10−64πϵ0(1a−1b)
This shows that the new potential difference is still proportional to the original potential difference V.
Since the potential difference depends only on the charges inside and the geometry, and the outer charge does not affect the potential difference, we conclude that the new potential difference remains the same:
Vnew=V
Topper's Solved these Questions
Similar Questions
A solid conducting sphere of radius a is enclosed in a concentric shell of radius b>a. The charge on the inner sphere is 3μC and on the conducting shell is −10μC. The potential difference between the conductors is V. If +10μC additional charge is given to the outer shell, the new potential difference is
A. V
B. V/2
C. 2V
D. zeroView SolutionA solid conducting sphere of radius 10cm is enclosed by a thin metallic shell of radius 20cm. A charge q=20μC is given to the inner sphere is connected to the shell by a conducting wire.
View SolutionIn the given figure there are two concentric shells find potential difference between spheres.
 View Solution
View SolutionA conducting sphere is enclosed by a hollow conducting shell. Initially the inner sphere has a charge Q while the outer one is uncharged. The potential difference between the two spherical surface is found to be V. later on the outer shell is given a charge -4Q. The new potential difference between the two surfaces is : (A) V (B) −V (C) −2V (D) 2V
View SolutionA solid metal sphere of radius R has a charg +2Q. A hollow spherical shell of radius 3R placed concentric with the frist sphere has net charge -Q.
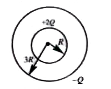
What would be the final distribution of charges if the sphres are joined by a conducting wireView SolutionA conducting shell S1 having a charge Q is surrounded by an uncharged concentric conducting spherical shell S2. Let the potential difference between S1 and that S2 be V. If the shell S2 is now given a charge −3Q, the new potential difference between the same two shells is
View SolutionA common test to find the genotype of a hybrid is by
View SolutionA solid conducting sphere of radius 'a' is surrounded by a thin uncharged concentric conducting shell of radius 2a. A point charge q is placed at a distance 4a from common centre of conducting sphere and shell. The inner sphere is then grounded
The charge on solid sphere isView SolutionA solid conducting sphere of radius 'a' is surrounded by a thin uncharged concentric conducting shell of radius 2a. A point charge q is placed at a distance 4a from common centre of conducting sphere and shell. The inner sphere is then grounded
Pick up the correct statement.View SolutionIf the electric potential of the inner shell is 10V and that of the outer shel is 5V, then the potential at the centre will be
 View Solution
View Solution
