If two tuning forks A & B give 4 beats/sec. with each other, on loading A with wax , 2 beats/sec. are given. If frequency of A is 256 Hz, then frequency of B is-
250 Hz
252 Hz
260Hz
262Hz
The correct Answer is:B
To solve the problem step by step, we need to analyze the information given and apply the concept of beats in sound waves.
1. Understanding Beats: The number of beats per second (beat frequency) is given by the absolute difference in frequencies of two tuning forks. If two tuning forks A and B produce 4 beats per second, we can express this mathematically as:
|fA−fB|=4 Hz
where fA is the frequency of tuning fork A and fB is the frequency of tuning fork B.
2. Given Frequency of A: We know that the frequency of tuning fork A, fA, is 256 Hz. Therefore, we can write:
|256−fB|=4
3. Finding Possible Frequencies for B: This equation can be solved to find the possible frequencies of tuning fork B:
- Case 1: 256−fB=4
fB=256−4=252 Hz
- Case 2: fB−256=4
fB=256+4=260 Hz
Thus, the possible frequencies for tuning fork B are 252 Hz and 260 Hz.
4. Effect of Loading A with Wax: When tuning fork A is loaded with wax, its frequency decreases. After loading, it produces 2 beats per second with tuning fork B. This means:
|f′A−fB|=2 Hz
where f′A is the new frequency of tuning fork A after loading with wax.
5. Calculating New Frequency of A: Since loading with wax decreases the frequency, we can denote the new frequency of A as:
f′A=256−x(where x is the decrease in frequency)
We need to find f′A to determine the new beat frequency with B.
6. Considering the Possible Frequencies: We can analyze both cases for fB:
- If fB=252 Hz:
|f′A−252|=2
This gives two scenarios:
- f′A=252+2=254 Hz (not possible since A's frequency decreases)
- f′A=252−2=250 Hz (possible)
- If fB=260 Hz:
|f′A−260|=2
This gives two scenarios:
- f′A=260+2=262 Hz (not possible since A's frequency decreases)
- f′A=260−2=258 Hz (possible)
7. Conclusion: Since the only valid scenario after loading A with wax is when fB=252 Hz and f′A=250 Hz, we conclude that the frequency of tuning fork B is:
fB=252 Hz
Final Answer:
The frequency of tuning fork B is 252 Hz.
|fA−fB|=4 Hz
where fA is the frequency of tuning fork A and fB is the frequency of tuning fork B.
|256−fB|=4
- Case 1: 256−fB=4
fB=256−4=252 Hz
- Case 2: fB−256=4
fB=256+4=260 Hz
|f′A−fB|=2 Hz
where f′A is the new frequency of tuning fork A after loading with wax.
f′A=256−x(where x is the decrease in frequency)
We need to find f′A to determine the new beat frequency with B.
- If fB=252 Hz:
|f′A−252|=2
This gives two scenarios:
- f′A=252+2=254 Hz (not possible since A's frequency decreases)
- f′A=252−2=250 Hz (possible)
- If fB=260 Hz:
|f′A−260|=2
This gives two scenarios:
- f′A=260+2=262 Hz (not possible since A's frequency decreases)
- f′A=260−2=258 Hz (possible)
fB=252 Hz
The frequency of tuning fork B is 252 Hz.
Topper's Solved these Questions
Similar Questions
If two tuning fork A and B are sounded together they produce 4 beats per second. A is then slightly loaded with wax, they produce 2 beats when sounded again. The frequency of A is 256. The frequency of B will be
View SolutionA tuning fork 'A' produces 6 beats per second with another fork 'B'. On loading 'B' with a little wax, it produces 5 beats per second with 'A'. If the frequency of 'A'is 256 Hz find the frequency of 'B?.
View Solution
Knowledge Check
IF two tuning forks A and B are sounded together, they produce 4 beats per second. A is then slightly loaded with wax, they produce two beats when sounded again. The frequency of A is 256. The frequency of B will be
A250B252C260D262A beat of 10 Hz is heard when two tuning forks A and B are sounded together. If a small piece of wax is fixed on B, the beat frequency decreae. iF A has a frequency of 200 Hz, then the frequency of B will be
A200 HzB190 HzC210 HzD195 Hz
Two tuning fork A and B are sounded together gives 5 beats per second. If frequency of B is 260 Hz and after loading A with was the beat frequency increases the frequency of A is
View SolutionA set of 24 tuming forka is arranged in series of Locrening frequencies. If each tuning fork gives 4 beats/sec with the preceding one and the last fork is found to be the octave of the first, calculate the frequences of the first and the last.
View SolutionA set of 10 tuning forks is arranged in series of increasing frequency. If each fork gives 3 beats with the preceding one and the last fork has twice the frequency of the first, then frequency of the first tuning fork is
View SolutionTuning fork A when sounded with a tuning for B of frequency 480 Hz gives 5 beats per second. When the prongs of A are loaded with wax, it gives 3 beats per second. The original frequency of A is
View SolutionA tuning fork P of unknows frequency gives 7 beats in 2 seconds with another tuning fork Q. When Q runs towards a wall with a speed of 5m/s it gives 5 beats per second with its echo. On loading P with wax, it gives 5 beats per second with Q . What is the frequency of P? Assume speed of sound = 332m/s .
View SolutionTwo tuning forks P and Q are vibrated together. The number of beats produced are represented by the straight line OA in the following graph. After loading Q with wax again these are vibrated together and the beats produced are represented by the line OB. If the frequency of P is 341 Hz, then frequency of Q will be
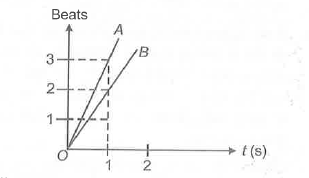
View Solution

