A square is made of four rods of same material one of the diagonal of a square is at temperature difference 100∘C, then the temperature difference of second diagonal:
0∘C
100l
1002l
100∘C
The correct Answer is:A
To solve the problem, we will analyze the heat transfer through the square made of four rods of the same material. We will denote the corners of the square as A, B, C, and D.
1. Identify the Given Information:
- We have a square with corners A, B, C, and D.
- The temperature difference along one diagonal (let's say BD) is given as TD−TB=100∘C.
2. Understand the Heat Flow:
- Since all rods are made of the same material, they have the same thermal resistance (R).
- The heat current (I) flowing through each rod can be expressed as:
I=ΔTR
- Here, ΔT is the temperature difference across the rod.
3. Set Up the Equations:
- For the diagonal BD:
IBD=TD−TBR
- For the diagonal AC:
IAC=TA−TCR
4. Equate the Heat Currents:
- Since the rods are identical, the heat current through each rod must be equal:
IBD=IAC
- This leads to:
TD−TBR=TA−TCR
- We can cancel R from both sides:
TD−TB=TA−TC
5. Substitute the Known Temperature Difference:
- We know TD−TB=100∘C, so we can substitute this into the equation:
100∘C=TA−TC
6. Conclusion:
- Rearranging gives us:
TA−TC=100∘C
- Therefore, the temperature difference along the second diagonal (AC) is also 100∘C.
Final Answer:
The temperature difference of the second diagonal (AC) is 100∘C.
---
- We have a square with corners A, B, C, and D.
- The temperature difference along one diagonal (let's say BD) is given as TD−TB=100∘C.
- Since all rods are made of the same material, they have the same thermal resistance (R).
- The heat current (I) flowing through each rod can be expressed as:
I=ΔTR
- Here, ΔT is the temperature difference across the rod.
- For the diagonal BD:
IBD=TD−TBR
- For the diagonal AC:
IAC=TA−TCR
- Since the rods are identical, the heat current through each rod must be equal:
IBD=IAC
- This leads to:
TD−TBR=TA−TCR
- We can cancel R from both sides:
TD−TB=TA−TC
- We know TD−TB=100∘C, so we can substitute this into the equation:
100∘C=TA−TC
- Rearranging gives us:
TA−TC=100∘C
- Therefore, the temperature difference along the second diagonal (AC) is also 100∘C.
The temperature difference of the second diagonal (AC) is 100∘C.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - Exercise-21videos
HEAT TRANSFER
- BOOK - RESONANCE ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - Exercise-31videos
HEAT TRANSFER
- BOOK - RESONANCE ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - Exercise-11videos
HEAT TRANSFER
- BOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise21videos
GRAVITATION
- BOOK - RESONANCE ENGLISHCHAPTER - KINEMATICSEXERCISE - Exercise65videos
KINEMATICS
Similar Questions
One diagonal of a square is 3x-4y+8=0 and one vertex is (-1,1), then the area of square is
View SolutionTwo diagonally opposite corners of a square made of a four thin rods of same material, same dimensions are at temperature 40∘C and 10∘C. If only heat conduction takes place, then the temperature difference between other two corners will be
View Solution
Knowledge Check
- Question 1 - Select One
A solid sphere and a hollow sphere of same material and size are heated to same temperature and allowed to cool in the same surroundings. If the temperature difference between each sphere and its surrounding is T, then
Athe hollow sphere will cool at a faster rate for all, values of TBthe solid sphere will cool at a faster rate for all value of TCboth spheres will cool at the same rate for all values of TDboth spheres will cool at the same rate only for small value of T. - Question 2 - Select One
A wall has two layers A and B, each made of different material. Both the layers have the same thickness. The thermal conductivity of the material of A is twice that of B . Under thermal equilibrium, the temperature difference across the wall is 36∘C. The temperature difference across the layer A is
A12.∘CB18.∘CC6.∘CD24.∘C
If one of the sides of a square is 3x-4y-12 = 0 and the center is (0,0), then find the equations of the diagonals of the square.
View SolutionIf one of the sides of a square is 3x−4y−12=0 and the center is (0,0) , then find the equations of the diagonals of the square.
View SolutionThe equation of one diagonal of a square is 2x+y=6 and its one vertex is (4,3). Find the equation of other diagonal.
View SolutionA different of temperature of 25∘C is equivalent to a difference of
View SolutionFour rods of same material and having the same cross section and length have been joined, as shown. The temperature of the junction of four rods will be :
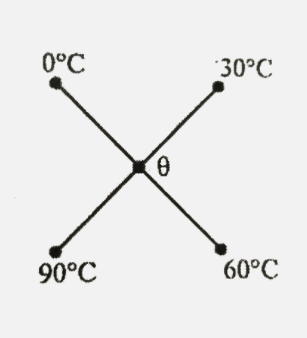 View Solution
View SolutionThe diagonal of a square is 15 m, find the length of its one side and perimeter.
View Solution
