The dimensions of a block are 1cm×1cm×100cm. If the specific resistance of its material is 2×10−7ohm×metre, then the resistance between the opposite rectangular faces is
2×10−9Ω
2×10−7Ω
2×10−5Ω
2×10−3Ω
The correct Answer is:B
To find the resistance between the opposite rectangular faces of the block, we can use the formula for resistance:
R=ρlA
where:
- R is the resistance,
- ρ is the specific resistance (resistivity) of the material,
- l is the length of the block (the distance between the two opposite faces),
- A is the cross-sectional area of the block.
Step 1: Identify the dimensions of the block
The dimensions of the block are given as:
- Length = 100 cm
- Width = 1 cm
- Height = 1 cm
Step 2: Convert dimensions to meters
To use the resistivity value given in ohm-meters, we need to convert all dimensions from centimeters to meters:
- Length l=100cm=100×10−2m=1m
- Width w=1cm=1×10−2m=0.01m
- Height h=1cm=1×10−2m=0.01m
Step 3: Calculate the cross-sectional area A
The cross-sectional area A is given by the product of width and height:
A=w×h=(0.01m)×(0.01m)=0.0001m2
Step 4: Use the specific resistance value
The specific resistance ρ is given as:
ρ=2×10−7Ω⋅m
Step 5: Substitute values into the resistance formula
Now we can substitute the values into the resistance formula:
R=ρlA=(2×10−7Ω⋅m)×(1m)0.0001m2
Step 6: Calculate the resistance
Calculating the above expression gives:
R=2×10−70.0001=2×10−710−4=2×10−3Ω
Final Answer
The resistance between the opposite rectangular faces is:
R=2×10−3Ω
---
- R is the resistance,
- ρ is the specific resistance (resistivity) of the material,
- l is the length of the block (the distance between the two opposite faces),
- A is the cross-sectional area of the block.
The dimensions of the block are given as:
- Length = 100 cm
- Width = 1 cm
- Height = 1 cm
To use the resistivity value given in ohm-meters, we need to convert all dimensions from centimeters to meters:
- Length l=100cm=100×10−2m=1m
- Width w=1cm=1×10−2m=0.01m
- Height h=1cm=1×10−2m=0.01m
The cross-sectional area A is given by the product of width and height:
A=w×h=(0.01m)×(0.01m)=0.0001m2
The specific resistance ρ is given as:
ρ=2×10−7Ω⋅m
Now we can substitute the values into the resistance formula:
R=ρlA=(2×10−7Ω⋅m)×(1m)0.0001m2
Calculating the above expression gives:
R=2×10−70.0001=2×10−710−4=2×10−3Ω
The resistance between the opposite rectangular faces is:
R=2×10−3Ω
Topper's Solved these Questions
Similar Questions
Dimensions of a block are 1cm×1cm×100cm. If specific resistance of its material is 3×10−7ohm−m, then the resistance between the opposite rectangular facesis
View SolutionDimensions of a block are 1cm×1cm×100cm. If specific resistance of its material is 3×10−7ohm−m, then the resistance between the opposite square faces is
View Solution
Knowledge Check
A wire of resistance 4Ω is used to wind a coil of radius 7 cm. The wire has a diameter of 1.4 mm and the specific resistance of its material is 2×10−7Ωm. Find the number of turns in the coil.
A50B40C60D70
A rectangular carbon block has dimensions 1.0cm×1.0×50cm.
(i) What is the resistance measured between the two square ends ?
(ii) Between two opposing rectangular faces ?
Resistivity of carbon at 20∘C is 3.5×10−5Ωm.
View SolutionThe dimensions of a wooden block are 1.1m×2.36mx3.1m. The number of significant figures in its volume should be
View SolutionA wire of resistance 10(Ω)is bent to form a complete circle.Find its resistance between two diametrically opposite points.
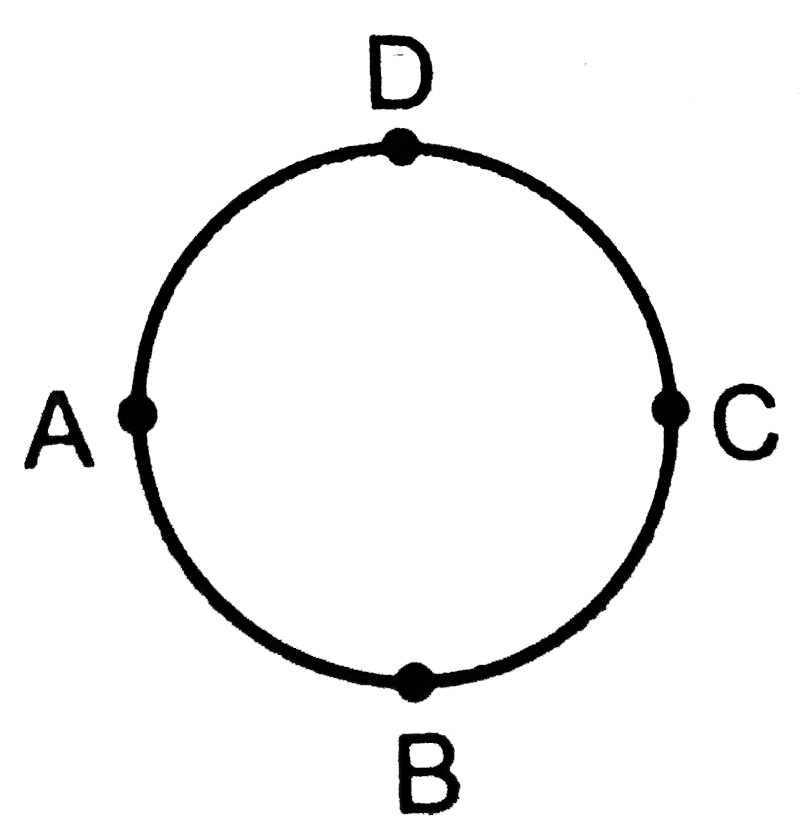
View SolutionA 0.1 M solution of monobasic acid at specific resistance of r ohms-cm, its molar conductivity is
View SolutionA rod of certain metal is 1.0m long and 0.6cm in diameter. Its resistance is 3.0×10&(−3) ohm. Another disc made of the same metal is 2.0cm in diameter and 1.0mm thick. What is the resistance between the round faces of the disc?
View SolutionA copper wire of cross - sectional area 3.4 mm2 and length of the wire 400m, specific resistivity of copper is 1.7×10−8Ω−m. Then the resistance of the wire is
View SolutionThe magnetic moment of a magnet (15cm×2cm×1cm)is1.2A−m2. Calculate its intensity of magnetisation
View Solution
