The displacement from the position of equilibrium of a point 4 cm from a source of sinusoidal oscillations is half the amplitude at the moment t=T/6 (T is the time perios). Assume that the source was at mean position at t=0. The wavelength of the running wave is :
A. 0.96 m
B. 0.48 m
C. 0.24 m
D. 0.12 m
0.96 m
0.48 m
0.24 m
0.12 m
The correct Answer is:B
To solve the problem, we need to find the wavelength of the running wave given the displacement from the equilibrium position at a certain distance and time. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the given information
- Displacement y at a distance x=4 cm from the source is half the amplitude A at time t=T6.
- Thus, we can write:
y=A2
Step 2: Use the wave equation
The general equation for a sinusoidal wave is given by:
y=Asin(ωt−kx)
Where:
- ω=2πT is the angular frequency,
- k=2πλ is the wave number.
Step 3: Substitute the known values
At t=T6 and x=4 cm (or 0.04 m), we substitute into the wave equation:
A2=Asin(2πT⋅T6−2πλ⋅0.04)
Step 4: Simplify the equation
Cancelling A from both sides (assuming A≠0):
12=sin(π3−8πλ)
Step 5: Solve for the sine value
We know that sin(π6)=12. Thus, we can set up the equation:
π3−8πλ=π6
Step 6: Rearranging the equation
Rearranging gives:
8πλ=π3−π6
Calculating the right side:
π3−π6=2π6−π6=π6
Step 7: Solve for λ
Now we have:
8πλ=π6
Cross-multiplying gives:
8π⋅6=πλ
Dividing both sides by π:
48=λ
Thus:
λ=0.48 m
Conclusion
The wavelength of the running wave is λ=0.48 m, which corresponds to option B.
---
- Displacement y at a distance x=4 cm from the source is half the amplitude A at time t=T6.
- Thus, we can write:
y=A2
The general equation for a sinusoidal wave is given by:
y=Asin(ωt−kx)
Where:
- ω=2πT is the angular frequency,
- k=2πλ is the wave number.
At t=T6 and x=4 cm (or 0.04 m), we substitute into the wave equation:
A2=Asin(2πT⋅T6−2πλ⋅0.04)
Cancelling A from both sides (assuming A≠0):
12=sin(π3−8πλ)
We know that sin(π6)=12. Thus, we can set up the equation:
π3−8πλ=π6
Rearranging gives:
8πλ=π3−π6
Calculating the right side:
π3−π6=2π6−π6=π6
Now we have:
8πλ=π6
Cross-multiplying gives:
8π⋅6=πλ
Dividing both sides by π:
48=λ
Thus:
λ=0.48 m
The wavelength of the running wave is λ=0.48 m, which corresponds to option B.
Topper's Solved these Questions
Similar Questions
If abody starts executing S.H.M. from mean position with amplitude 'A', maximum velocity v0 and time period 'T', then the correct statemens are (x is displacement from mean position)
View SolutionFigure shows a snapshot of a sinusoidal travelling wave taken at t=0.3s.The wavelength is 7.5cm and the amplitude is 2cm. If the crest P was at x=0at t=0, write the equation of travelling wave. ,

View SolutionTwo points are located at a distance of 10m and 15m from the source of oscillation. The period of oscillation is 0.05s and the velocity of the wave is 300m/s. What is the phase difference between the oscillation of two points?
View SolutionThe time period of a particle executing SHM is T. After a time T/6 after it passes its mean position, then att=0 its :
View SolutionThe time period of a particle in simple harmonic motion is T. Assume potential energy at mean position to be zero. After a time of T6 it passes its mean position ,then at t=0 its,
View SolutionA 10 W source of sound of frequency 1000 Hz sends out wave in air. The displacment amplitude at a distance of 10 m from the source is
(speed of sound in air = 340 m/s and density of air = 129 kgm3)
(A)0.62μm (B)4.2μm (C)1.6μm (D)0.96μm
View SolutionA particle executes simple harmonic oscillation with an amplitudes a. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude from the equilibrium position is
View SolutionA particle executes simple harmonic oscillation with an amplitudes a. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude from the equilibrium position is
View SolutionThe plot shows the position (x) as a function of time (t) for two trains that run on a parallel track. Train A is next to train B at t=0 and at t=T0.

View SolutionThe acceleration of particle varies with time as shown.
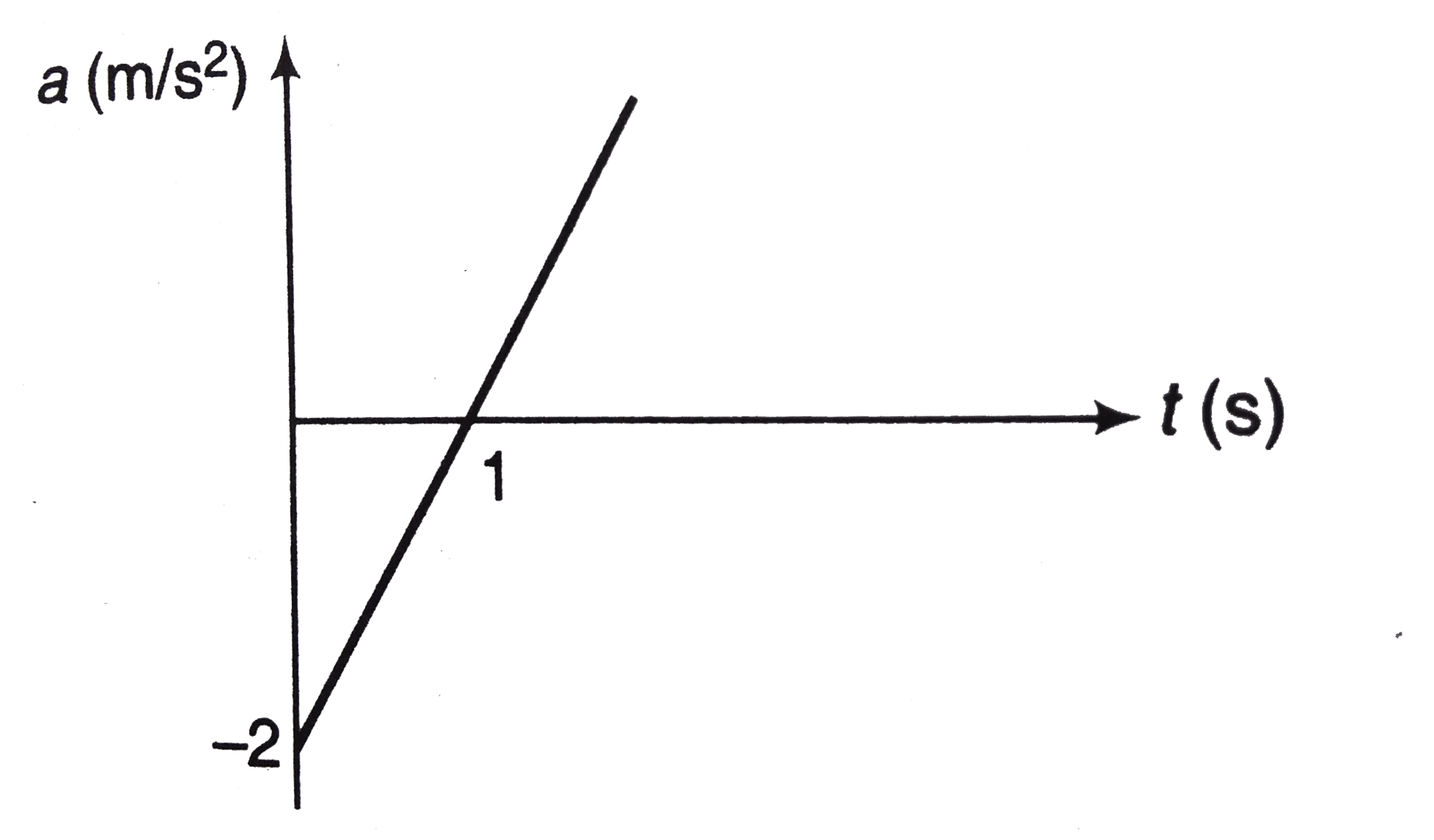
(a) Find an expression for velocity in terms of t.
(b) Calculate the displacement of the particle in the interval from t=2s to t=4s. Assume that v=0 at t=0.
View Solution
