A particle P collides with 15ms−1 at an angle 60∘ from vertical on smooth horizontal surface. The coefficient of restitution (e) is 1√3. The range R, as shown in diagram will be : [Take g=10m/s2]
![A particle P collides with 15 ms^(-1) at an angle 60^(@) from vertical on smooth horizontal surface. The coefficient of restitution (e) is (1)/(sqrt(3)). The range R, as shown in diagram will be : [Take g =10 m//s^(2)]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RES_DPP_PHY_XII_E01_923_Q01.png)
12.5 m
12 mm
11.25 m
12.75 m
The correct Answer is:C
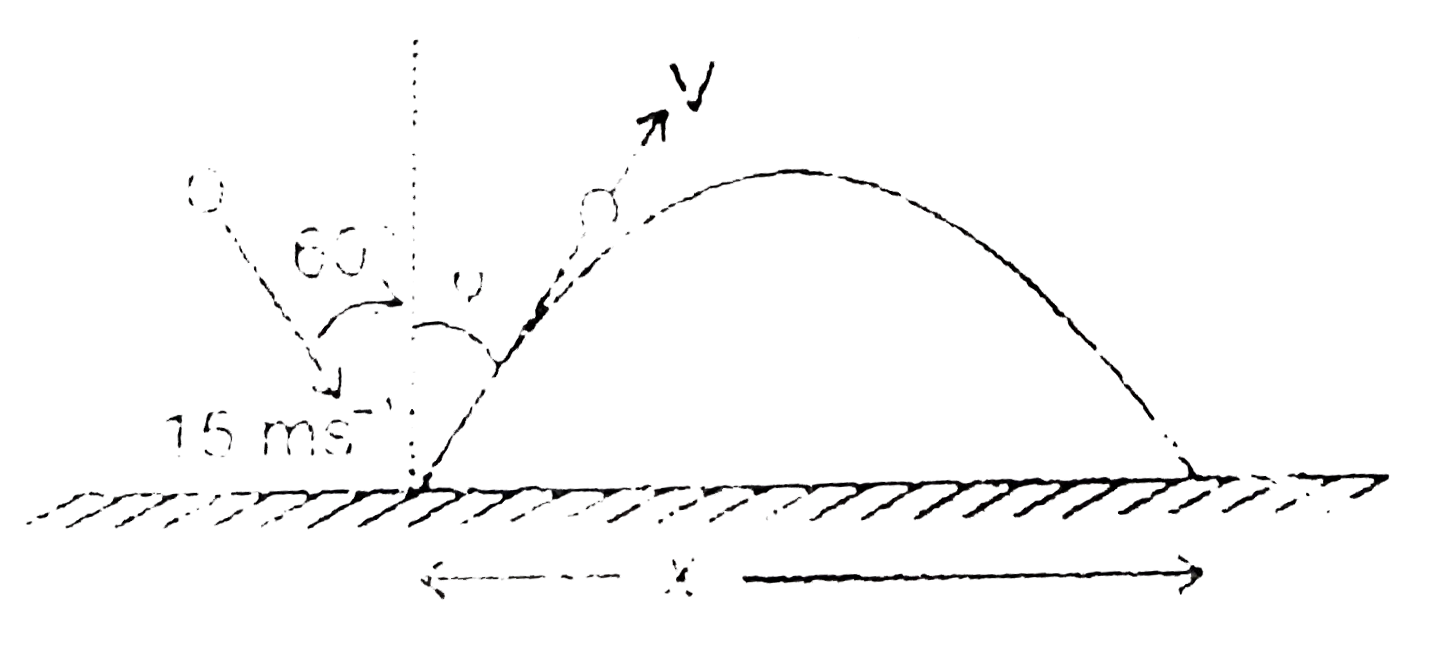
Given e=1√3tanϕ=1etanθ
tanϕ=3⇒sinϕ=3√10
Along horizontal, m×15sin60∘=m×vsinϕ
m×15sin60∘=m×vsinϕ
v=15√5√102×3=13.7ms−1
x=v2sin2(π2−ϕ)g=v2sin2ϕg
=(13.7)2×2×31010=11.25m
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.65
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.66
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.63
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
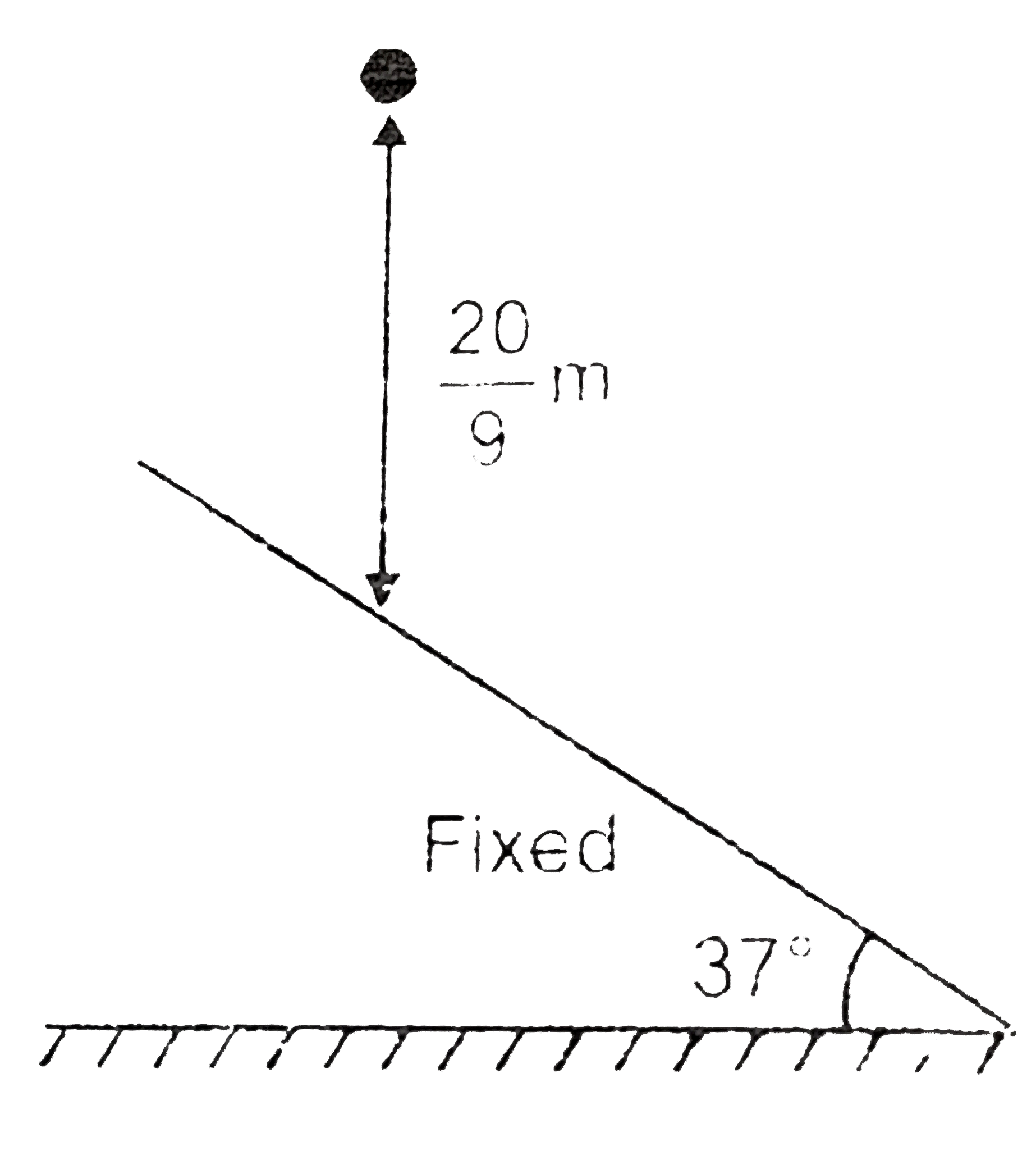
A ball is dropped on a large smooth inclined plane of angle of inclination 37∘, from a height of 209m above the point of impact. The coefficient of restitution of the impact is e=916 then :
[Take g=10m/s2]
View SolutionA projectile is thrown with a velocity of 10ms−1 at an angle of 60∘ with horizontal. The interval between the moments when speed is √5gm/s is (Take, g=10ms−2)
View SolutionA particle of mass m moving with a speed u strikes a smooth horizontal surface at an angle 45∘. The particle rebounds at an angle ϕ with speed v. If coefficient of restituion is 1√3, then angle ϕ is
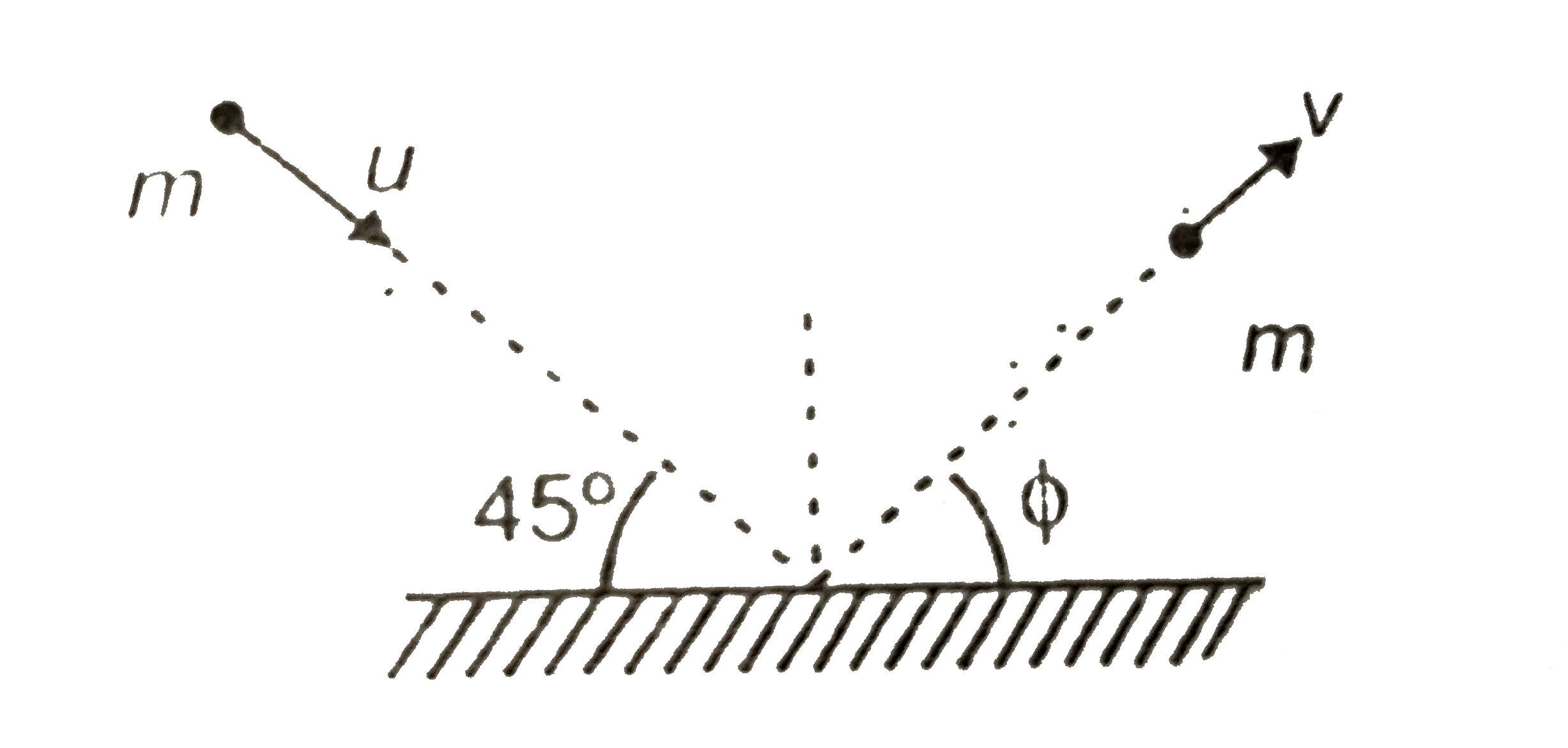
View SolutionA particle of mass m moving with a speed u strikes a smooth horizontal surface at an angle 45∘. The particle rebounds at an angle ϕ with speed v. If coefficient of restituion is 1√3, then angle ϕ is

View SolutionA ball moving with speed v collides with a horizontal smooth surface at an angle θ with normal to surface as shown in figure. If coefficient of restitution of collision is e, then find v'

View SolutionA projectile is launched with a speed of an angle 60∘ with the horizontal from a sloping surface of inclination 30∘. The range R is: (g=10m/s2)
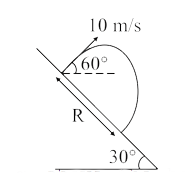
View SolutionA stone is thrown with a speed of 10ms−1 at an angle of projection 60∘. Find its height above the point of projection when it is at a horizontal distance of 3m from the thrower ? (Take g=10ms−2)
View SolutionA stone is thrown with a speed of 10ms−1 at an angle of projection 60∘. Find its height above the point of projection when it is at a horizontal distance of 3m from the thrower ? (Take g=10ms−2)
View SolutionA particle is projected with a speed 10√2ms−1 and at an angle 45∘ with the horizontal. The rate of change of speed with respect to time at t=1s is (g=10ms−2)
View SolutionA particle collides with a smooth, surface with speed u at an angle θ. Coefficient of restitution is e. Find the ratio of the horizontal ranges of two consecutive projectile motions
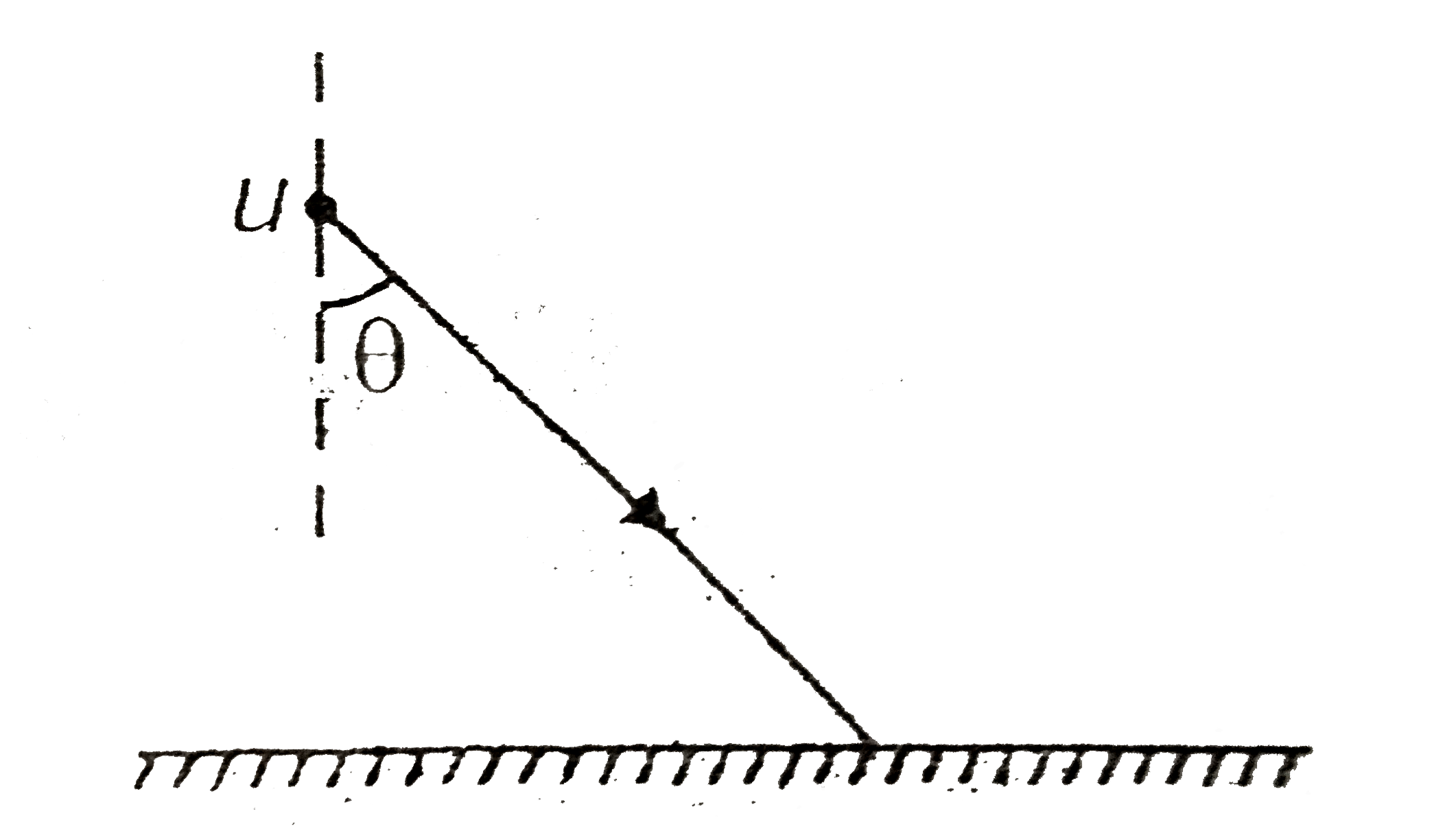
View Solution

