Two balls of same mass are released simultaneously from heights h & 2h from the ground level. The balls collide with the floor & stick to it. Then the velocity-time graph of centre of mass of the two balls is best represented by :
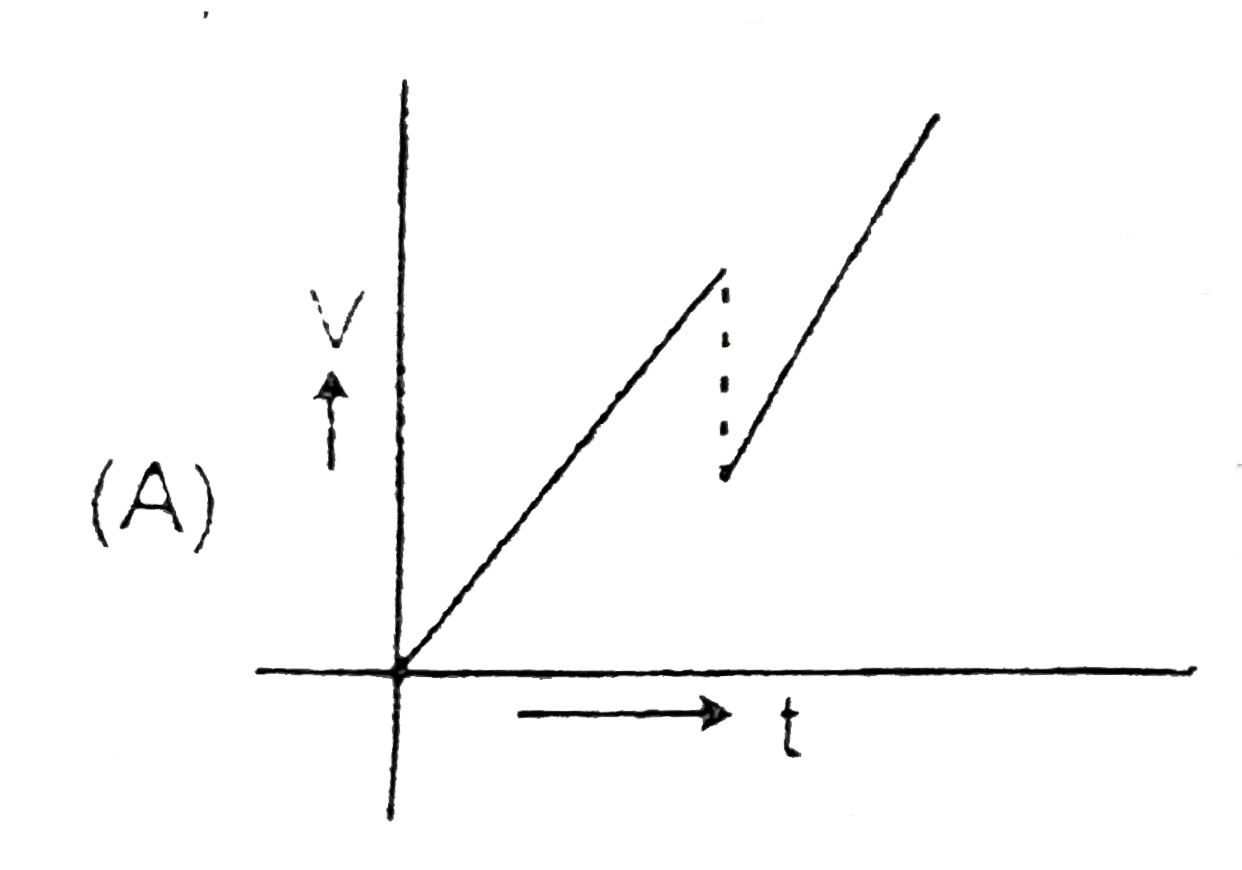



The correct Answer is:B
To solve the problem, we need to analyze the motion of the two balls released from different heights and determine the velocity-time graph of their center of mass after they collide with the ground.
1. Identify the Initial Conditions:
- Let the mass of each ball be m.
- The first ball is released from height h.
- The second ball is released from height 2h.
2. Calculate the Time of Flight for Each Ball:
- For the first ball (height h):
h=12gt21⟹t1=√2hg
- For the second ball (height 2h):
2h=12gt22⟹t2=√4hg=2√hg
3. Determine the Velocities Just Before Impact:
- For the first ball:
v1=gt1=g√2hg=√2gh
- For the second ball:
v2=gt2=g(2√hg)=2√gh
4. Behavior Upon Collision:
- When the balls hit the ground, the first ball comes to rest, so its velocity becomes 0.
- The second ball also comes to rest after colliding with the ground.
5. Calculate the Velocity of the Center of Mass (CM):
- The velocity of the center of mass before the collision can be calculated using:
vcm=mv1+mv2m+m=v1+v22=√2gh+2√gh2=(1+√2)√gh2
- After the collision, the first ball's velocity is 0 and the second ball's velocity is also 0:
vcm_after=m⋅0+m⋅0m+m=0
6. Graphing the Velocity-Time Relation:
- Initially, the center of mass has a certain velocity (calculated above) and then drops to 0 after the collision.
- The graph will show a linear decrease from the initial velocity to 0 at the time of collision.
Conclusion:
The velocity-time graph of the center of mass will show a linear decrease in velocity from a positive value to 0 after the collision.
- Let the mass of each ball be m.
- The first ball is released from height h.
- The second ball is released from height 2h.
- For the first ball (height h):
h=12gt21⟹t1=√2hg
- For the second ball (height 2h):
2h=12gt22⟹t2=√4hg=2√hg
- For the first ball:
v1=gt1=g√2hg=√2gh
- For the second ball:
v2=gt2=g(2√hg)=2√gh
- When the balls hit the ground, the first ball comes to rest, so its velocity becomes 0.
- The second ball also comes to rest after colliding with the ground.
- The velocity of the center of mass before the collision can be calculated using:
vcm=mv1+mv2m+m=v1+v22=√2gh+2√gh2=(1+√2)√gh2
- After the collision, the first ball's velocity is 0 and the second ball's velocity is also 0:
vcm_after=m⋅0+m⋅0m+m=0
- Initially, the center of mass has a certain velocity (calculated above) and then drops to 0 after the collision.
- The graph will show a linear decrease from the initial velocity to 0 at the time of collision.
The velocity-time graph of the center of mass will show a linear decrease in velocity from a positive value to 0 after the collision.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.59
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.60
Explore 8 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.57
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
Two balls are thrown simultaneously in air. The acceleration of the centre of mass of the two balls while in air
View SolutionTwo balls of equal mass are projected from a tower simultaneously with equal speeds. One at angle θ above the horizontal and the other at the same angle θ below the horizontal. The path of the center of mass of the two balls is
View SolutionA ball is thrown upwards with a speed u from a height h above the ground.The time taken by the ball to hit the ground is
View SolutionTwo balls are dropped from heights h and 2h respectively from the earth surface. The ratio of time of these balls to reach the earth is.
View SolutionTwo balls of same mass are dropped from the same height h, on to the floor. The first ball bounces to a height h/4, after the collision & the second ball to a height h/16. The impulse applied by the first & second ball on the floor are I1 and I2 respectively. Then :-
View SolutionA ball is projected upwards from a height h above the surface of the earth with velocity v. The time at which the ball strikes the ground is
View SolutionA ball is projected upwards from a height h above the surface of the earth with velocity v. The time at which the ball strikes the ground is
View SolutionA ball of mass 'm is released from the top of a smooth movable wedge of mass 'm'. When the ball collides with the floor, velocity is 'v'. Then the maximum height attained by the ball after an elastic collision with the floor is : (Nelect any edge at the lower end of the wedge)
View SolutionTwo identical balls are set into motion simultaneously from an equal height h. While ball A is thrown horizontally with velocity v, ball B is just released to fall by itself. Choose the alternative that best represents the motion of A and B with respect to an observer who moves with velocity v/2 with respect to the ground as shown in the figure.

View SolutionAn iron ball and a wooden ball of the same radius are released from a height ‘ h ’ in vacuum. The time taken by both of them to reach the ground is
View Solution
