A body of mass m is thrown straight up with velocity v0(v0<<ve) Find the velocity v with which the body comes down if the air drag equals kv2, where k is a positive constant and v is the velocity of the body.
The correct Answer is:A, B
A body of mass m is thrown straight up with velocity v0(V0<<ve) Find the velocity v' with which the body comes down it the air drag equals kv2 where k is a positive constant and v is the velocity of the body.
v=v0/√1+kv20/mg.
Related Playlists
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.3120videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.329videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.2920videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
A particle of mass m is projected upword with velocity v=ve2 (ve) escape of the particle is
View SolutionA body of mass m is thrown upwards at an angle θ with the horizontal with velocity v. While rising up the velocity of the mass after t second will be
View SolutionA smooth sledge is moving with constant velocity v0 toward left. A block is pushed toward right with a velocity v0’ (relative to ground).

(A) Find the velocity with which the block escapes from the sledge and necessary critical v0 for escaping from the sledge
(B) Will the block launch onto the sledge again?View SolutionA particle having a velocity v=v0 at t=0 is decelerated at the rate |a|=α√v, where α is a positive constant.
View SolutionA body is thrown with a velocity equal to n times the escape velocity (ve). Velocity of the body at large distance away will be :-
View Solution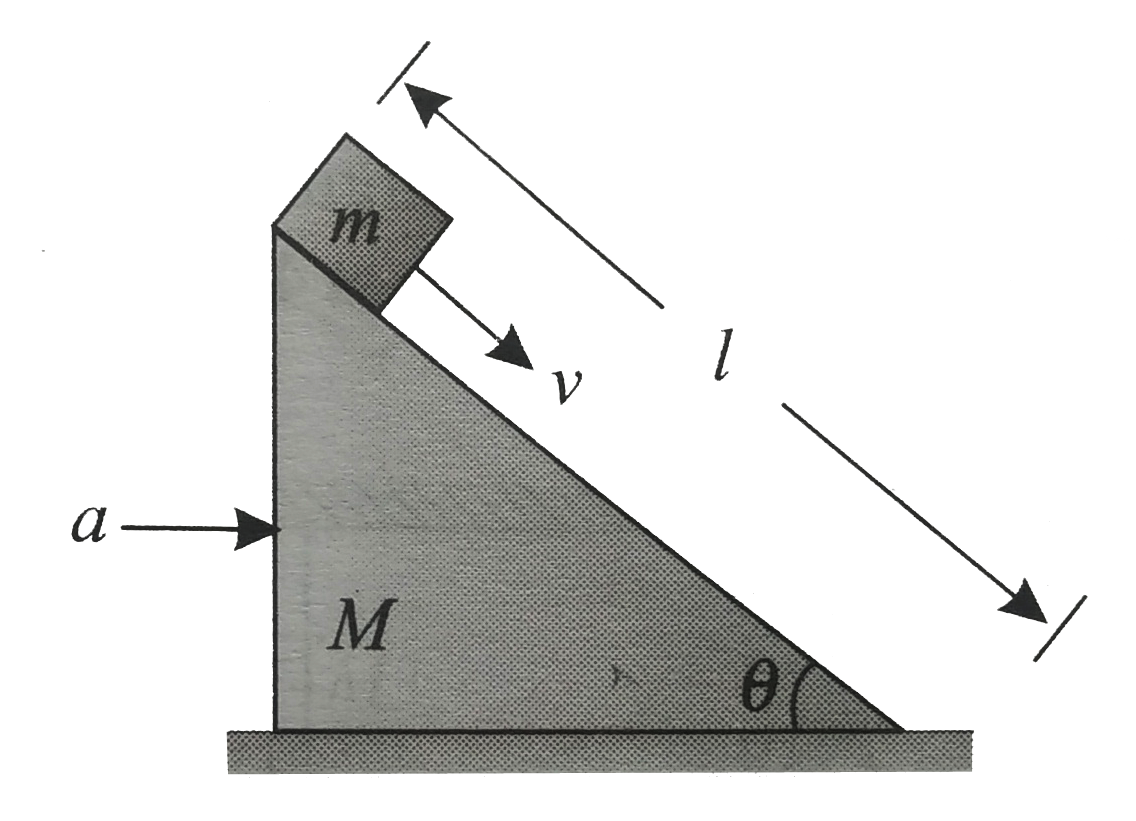
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
The horizontal force applied on the wedge is:View SolutionA motor boat of mass m moves along a lake with velocity v0. At t = 0, the engine of the boat is shut down. Resistance offered to the boat is equal to σv2. Then distance covered by the boat when its velocity becomes v0/2 is
View SolutionBlock B moves to the right with a constant velocity v0. The velocity of body a relative to b is
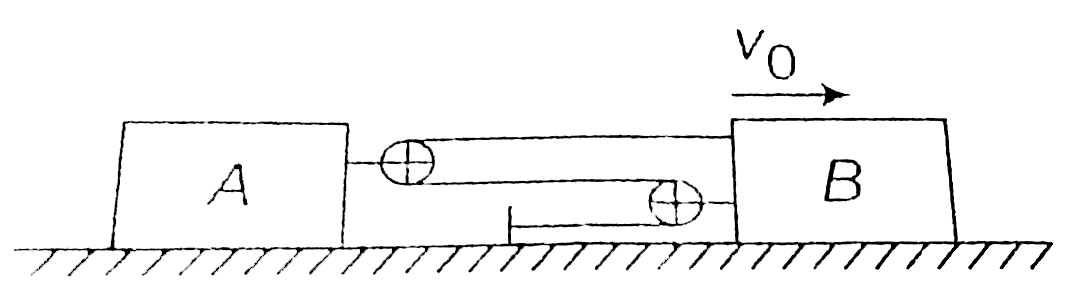 View Solution
View SolutionA body of mass m2 moving with velocity v0 collides elastically with another mass of m3 . Find % change in KE of first body
View SolutionA particle of mass m is projected upwards with velocity v=ve2, where ve is the escape velocity then at the maximum height the potential energy of the particle is : (R is radius of earth and M is mass of earth)
View Solution


