Work done by force F to move block of mass from A to C very slowly is . Force F is always acting tengetial to path. Equation of path AB is and BC is straight line which is tengent on curve AB at point B ( between block and path ABC is 0.5). then value of is
![Work done by force F to move block of mass 2 kg from A to C very slowly is (76 lambda)J. Force F is always acting tengetial to path. Equation of path AB is x^(2)=8y and BC is straight line which is tengent on curve AB at point B (mu between block and path ABC is 0.5). then value of lambda is [g=10 m//s^(2)]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RES_DPP_PHY_04_E01_030_Q01.png)
Slope of line
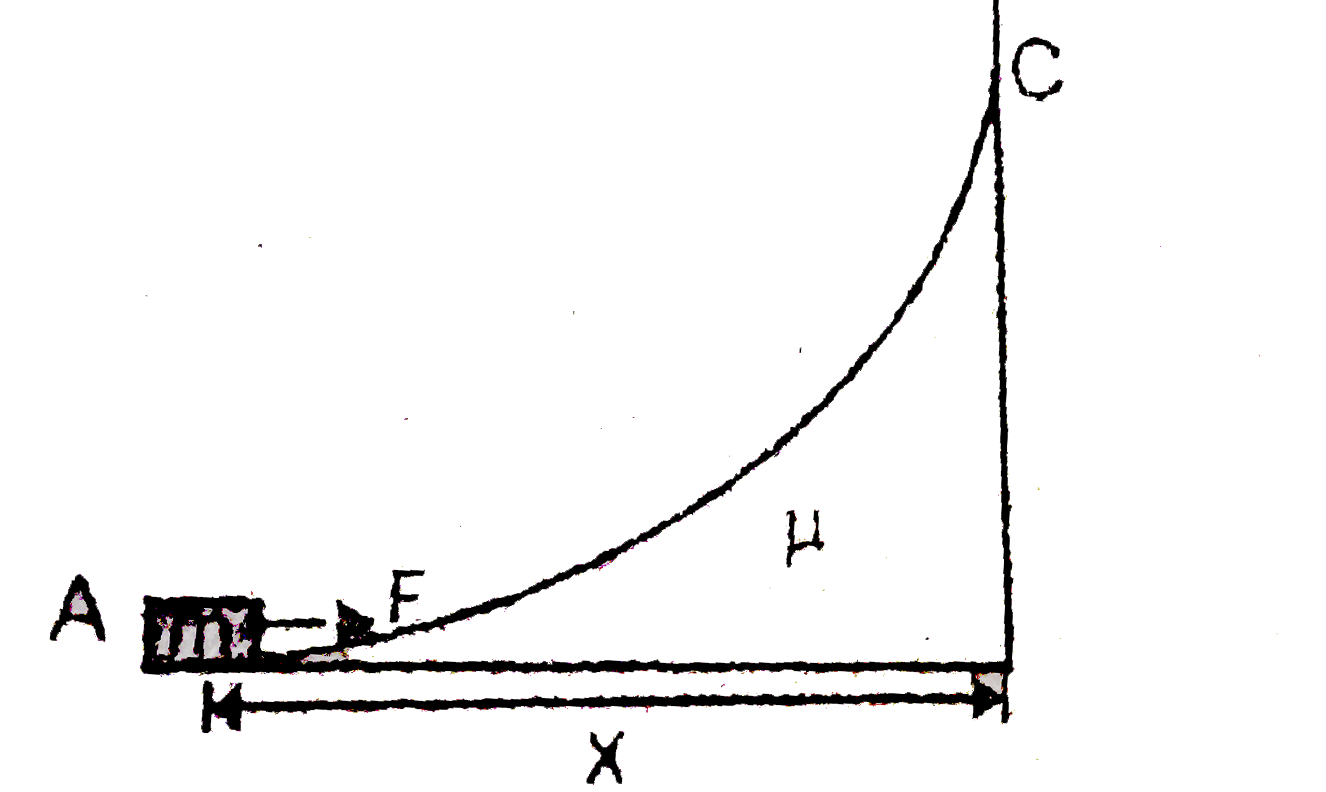
If the mass m is taken from A to C slowly work done by friction will always be equal to the

Now, by
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.25
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.26
Explore 8 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.23
Explore 20 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
Work done by force F to move block of mass 2kg from A to C very slowly is (76λ)J. Force F is always acting tangential to path. Equation of path AB is x2=8y and BC is straight line which tangent on curve AB to Point B (μ between block and path ABC is 0.5). Then value of 'λ' is [g=10m/s2]
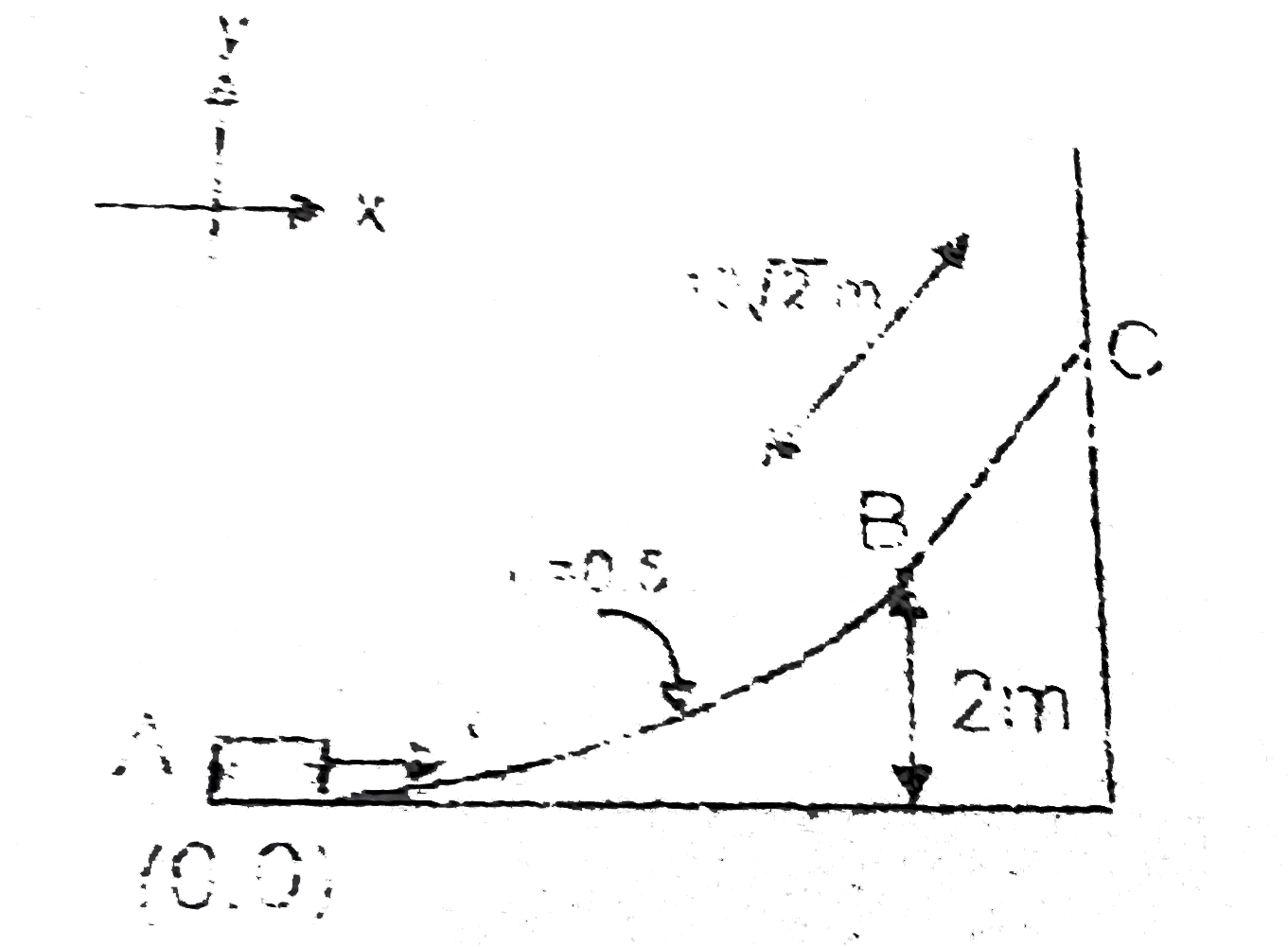
View SolutionA block of mass 10kg is placed on a horizontal surface as shown in the figure and a force F=100N is applied on the block as shown, in the figure. The block is at rest with respect to ground. If the contact force between block and ground is 25n (in Newton) then value of n is : (Takeg=10m/s2)

View Solution
Knowledge Check
A block of mass 2 kg initially at rest moves under the action of an applied horizontal force of 6 N on a rough horizontal surface. The coefficient of friction between block and surface is 0.1. The work done by the applied force in 10 s is (Take g=10ms−2)
A200JB−200JC600 JD−600JA block of mass m=2kg is resting on a rough inclined plane of inclination of 30∘ as shown in figure. The coefficient of friction between the block and the plane is μ=0.5. What minimum force F should be applied perpendicular to the plane on the block, so that blocks does not slip on the plane? (g=10m/s2)
 A2.68 NBZeroC4.34 ND6.24 N
A2.68 NBZeroC4.34 ND6.24 N
A block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
View SolutionA force bar F = (3hat i-4 hat j +b hat k)N is acting on the particle which is moving from point A ( 0-1, 1) m to the point B(2, 2 3) m If net work done by the force on the particle is zero then value of b is
View SolutionA force of 200N is applied as shown in the figure on block of 3 kg. The coefficient of friction between the block and the wall is 0.3. Find the friction acting on the block. (in N) {Take g = 10 m/s2

View SolutionLet L be the line belonging to the family of straight lines (a+2b) x+(a-3b)y+a-8b =0, a, b ∈R, which is the farthest from the point (2, 2).
If L is concurrent with the lines x-2y+1=0 and 3x−4y+λ=0, then the value of λ is
View SolutionA block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
View SolutionA block pulley arrangement is shown in the figure. If f1andf2 represents frictional force acting on the block A and B respectively then choose the correct statement. (given g=10m/s2)
View Solution