A small object stuck on the surface of a glass sphere (n=1.5) is viewed from the diametrically opposite position. Find transverse magnification.
The correct Answer is:3
To solve the problem of finding the transverse magnification of a small object stuck on the surface of a glass sphere (with a refractive index n=1.5) when viewed from the diametrically opposite position, we can follow these steps:
Step 1: Understand the setup
We have a glass sphere with a refractive index n=1.5. The object is located on the surface of the sphere, and we are viewing it from the opposite side of the sphere.
Step 2: Use the lens maker's formula
We can use the formula for refraction at a spherical surface, which is given by:
n2v−n1u=n2−n1R
where:
- n1 is the refractive index of the medium from which the light is coming (air, n1=1),
- n2 is the refractive index of the glass sphere (n2=1.5),
- u is the object distance (which is negative since the object is on the surface of the sphere),
- v is the image distance,
- R is the radius of the sphere (positive since we consider the radius of curvature).
Step 3: Assign values
For our case:
- The object is on the surface of the sphere, so u=−R (the object is at the surface),
- The radius of the sphere is R.
Step 4: Substitute into the formula
Substituting the values into the formula:
1.5v−1−R=1.5−1R
This simplifies to:
1.5v+1R=0.5R
Step 5: Rearranging the equation
Rearranging gives:
1.5v=0.5R−1R
1.5v=−0.5R
v=−1.5R0.5=−3R
Step 6: Calculate the magnification
The transverse magnification m is given by:
m=n1vn2u
Substituting the values:
m=1⋅(−3R)1.5⋅(−R)=−3R−1.5R=31.5=2
Final Result
Thus, the transverse magnification is:
m=2
We have a glass sphere with a refractive index n=1.5. The object is located on the surface of the sphere, and we are viewing it from the opposite side of the sphere.
We can use the formula for refraction at a spherical surface, which is given by:
n2v−n1u=n2−n1R
where:
- n1 is the refractive index of the medium from which the light is coming (air, n1=1),
- n2 is the refractive index of the glass sphere (n2=1.5),
- u is the object distance (which is negative since the object is on the surface of the sphere),
- v is the image distance,
- R is the radius of the sphere (positive since we consider the radius of curvature).
For our case:
- The object is on the surface of the sphere, so u=−R (the object is at the surface),
- The radius of the sphere is R.
Substituting the values into the formula:
1.5v−1−R=1.5−1R
This simplifies to:
1.5v+1R=0.5R
Rearranging gives:
1.5v=0.5R−1R
1.5v=−0.5R
v=−1.5R0.5=−3R
The transverse magnification m is given by:
m=n1vn2u
Substituting the values:
m=1⋅(−3R)1.5⋅(−R)=−3R−1.5R=31.5=2
Thus, the transverse magnification is:
m=2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.11
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.12
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.9
Explore 20 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
A mark on the surface of a glass spehre (μ=1.5) is viewed from a diametrically opposite position. It appears to be at a distance 10 cm from its actual position. The radius of the sphere is
View SolutionA glass sphere of diameter 50 cm and μ=1.5 has a small air bubble. Looking from outside the diameter, the bubble appears to be at a distance 10 cm the surface. Find the apparent position of the bubble when it is viewed from the diametrically opposite position.
View Solution
Knowledge Check
A mark placed on the surface of a sphere is viewed through glass from a position directly opposite. If the diameter of the sphere is 10cm and refractive index of glass is 1.5, find the position of the image.
A−20cmB30cmC40cmD−10cm
A glass shere of radius 2R, refractive index n has a spherical cavity of radius R, concentric with it. A black spot on the inner surface of the hollow sphere is viewed from the left as well as right. Obtain the shift in position of the object.
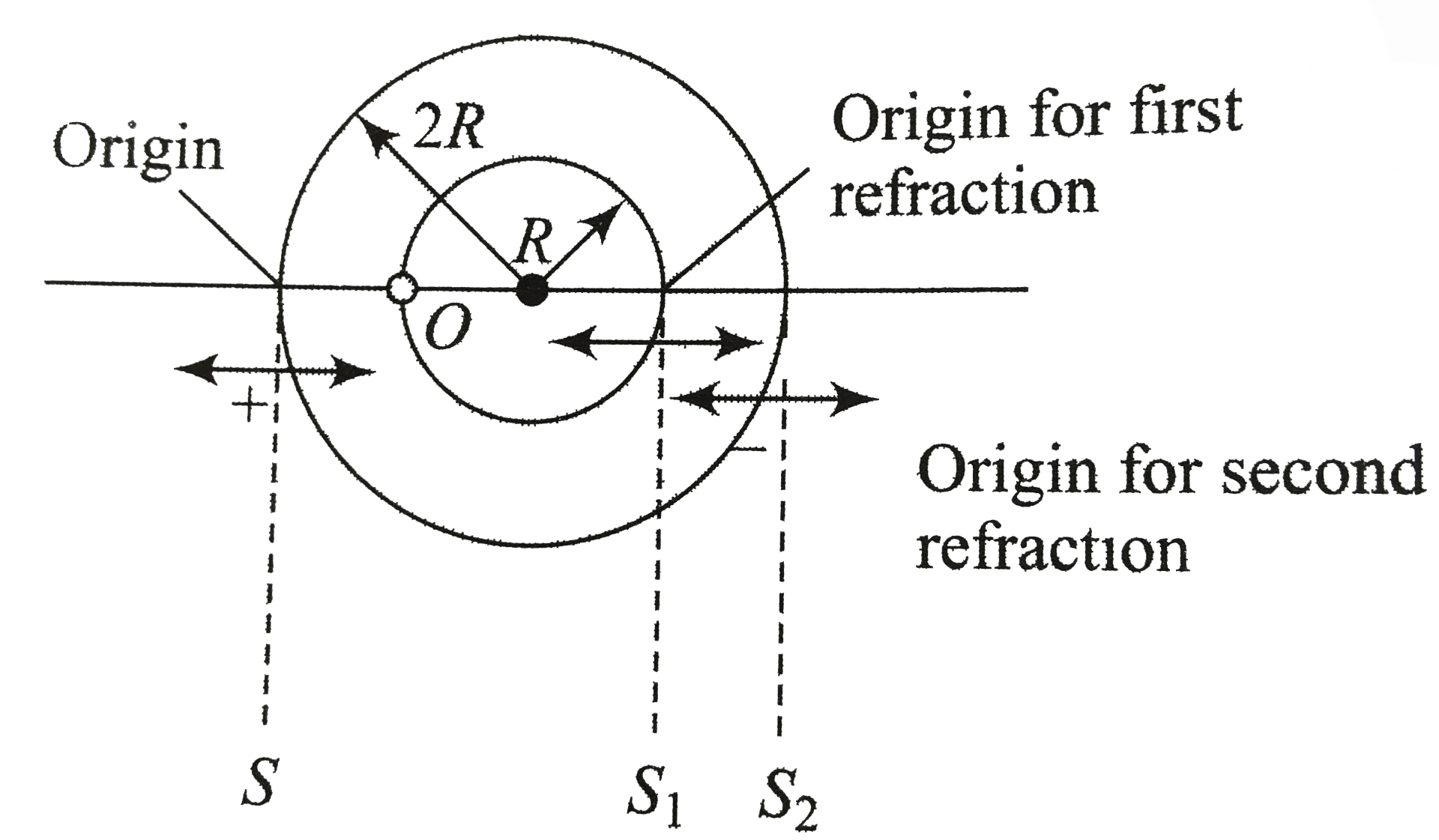
View SolutionA hemispherical portion of the surface of a solid glass sphere (mu = 1.5) of radius r is silvered to make the inner side reflecting. An object is placed on the axis of the hemisphere at a distance 3r from the centre of the sphere. The light from the object is refracted at the unsilvered part, then reflected from the silvered part and again refracted at the unsilvered part. Locate the final image formed.
View Solution
A spherical mirror is obtained as shown in the figure from a hollow glass sphere. If an object is positioned in front of the mirror, what will be the nature and magnification of the image of the object ? (Figure drawn as schematic and not to scale )
View SolutionA tranparent sphere of radius 20cm and refractive index 1.6 is fixed in a hole of the partition separating the two media: A(refractive index n1=1.2) and B ( refractive index n3=1.7). A luminous point object is placed 120cm from the surface of the sphere iin medium A. it is viewed from D in medium B in a direction normal to the sphere. Find the position of the image formed by the rays, from point N.

View SolutionA small air bubble is situated at a distance of 3 cm from the center of a glass sphere of radius 9 cm. When viewed from the nearest side, the bubble appears to be at a distance of 5 cm from the surface. Its apparent distance when viewed from the farthest side is n×5 cm where n is?
View SolutionAn air bubble is seen inside a solid sphere of glass (n=1.5) of 4.0cm diameter at a distance of 1.0cm from the surface of the sphere (on seeing along the diameter). Determine the real position of the bubble inside the sphere.
View SolutionA spider is on the surface of a glass sphere with a refractive inndex of 1.5 . An insect crawls on the other side of the sphere as shown in Fig. For what maximum value of θ will the spider be able to still see the insect. Assume the spiders eye is in air.
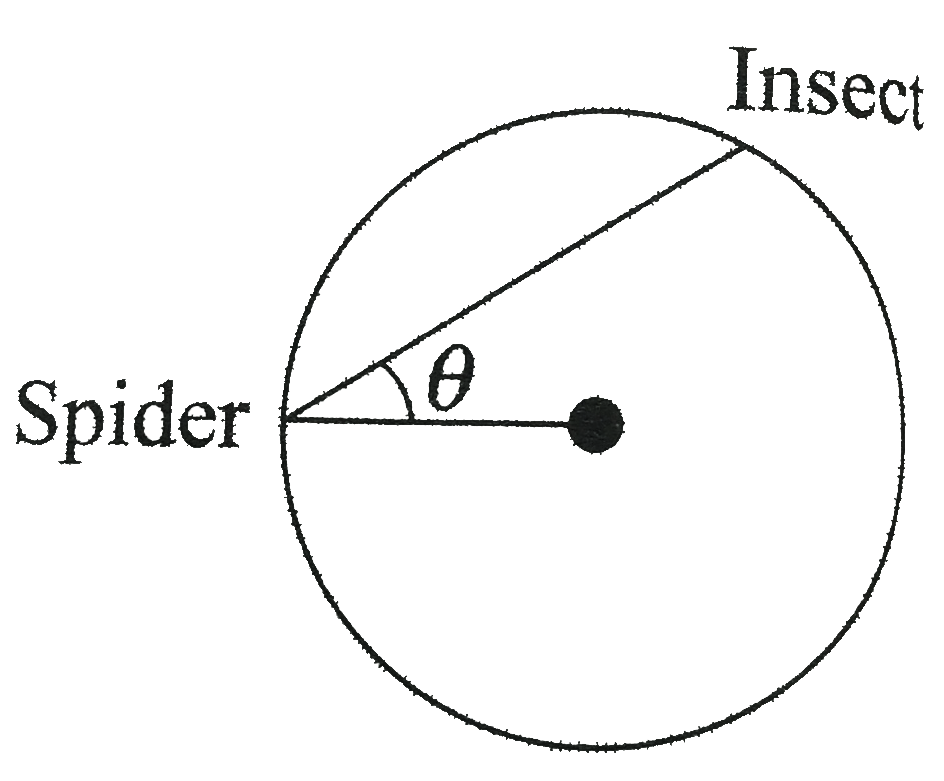
View Solution