The internal surface of the walls of a sphere is specular. The radius of the sphere is R=36cm. A point source S is placed at a distance R/2 from the cneter of the sphere and sends light to the remote part of the sphere. Where will the image of the source be after two successive reflections from the remote and then nearest wall of the sphere? How will the position of the image change if the source sends light to the nearest wall first?Consider paraxial rays.
The correct Answer is:Image will be at −5R6 from near end towards souce ; image will be at - (R)/(2) from remote end
Case- I

Applying mirror formula for remote pair
(u=−3R2,f=−R2)
⇒v=ufu−f=−34R
Now consider reflection from the nearer part for nearer part
u=3R4−2R=−5R4⇒v=−5R6
Case II
Consider reflection form nearer part first
u=−R2
v=ufu−f=−34R
Now consider reflection from the nearer part for nearer part
u=3R4−2R=−5R4⇒v=−5R6
Case II
Consider reflection from nearer part first
u=−R2
v=ufu−f=∞
Reflection from remote part gives v=−R2
Image will be at −5R6 from near end towards source , image will be at −R2 from remote end.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.9
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.10
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.7
Explore 20 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
A point charge q is placed at a distance of r from cebtre of an uncharged conducting sphere of rad R(<r). The potential at any point on the sphere is
View SolutionA point charge q , is placed at a distance r from the centre of an aluminium sphere, of radius R (r>R) . Selectr the correct alternatives.
View SolutionA hollow metal sphere of radius 5 cm is charged such that the potential on its surface is 10V. The potential at the distance 3cm from the centre of the sphere is:
View SolutionFind the radius of the sphere whose surface area is 36πcm2.
View SolutionThe diameter of a hollow metallic sphere is 60 cm and the sphere carries a charge of 500μC. The potential at a distance of 100cm from the centre of the sphere will be
View SolutionA point object is situated at a distance of 36 cm from the centre of the sphere of radius 12 cm and refractive index 1.5. Locate the position of the image due to refraction through sphere.
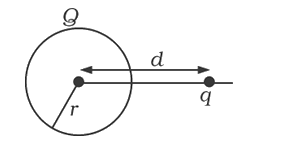
View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :
View SolutionA parallel beam of light emerges from the opposite surface of the sphere when a point source of light lies at the surface of the sphere. The refractive index of the sphere is
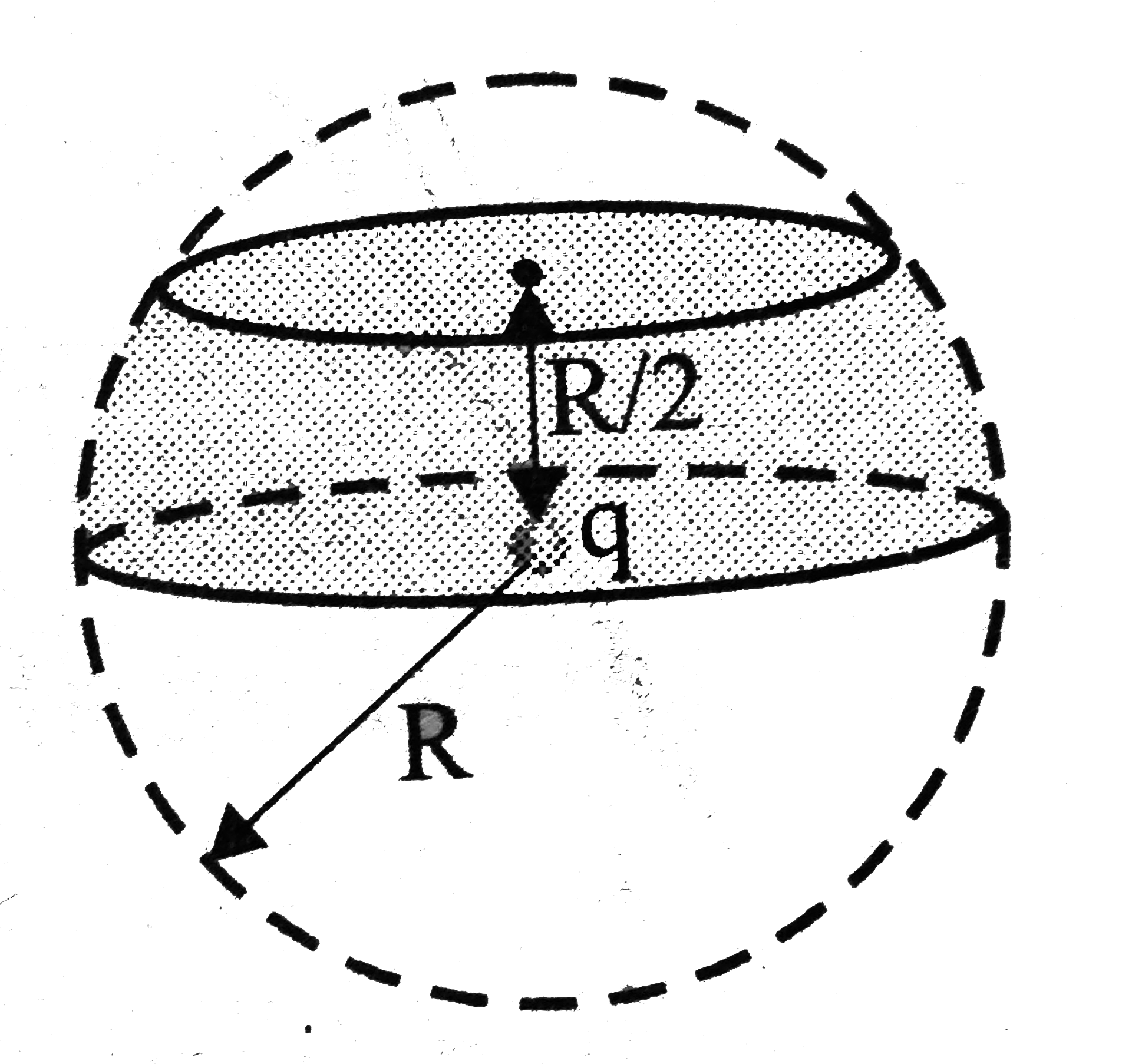
View SolutionFlux passing through the shaded surface of a sphere when a point charge q is placed at the center is (radius of the sphere is R)
View SolutionA conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View Solution

