The rate of change of angular momentum of a system of particles about the centre of mass is equal to the sum of external torque about the centre of mass when the centre of mass is :
Fixed with respect to an inertial frame.
in linear acceleration.
in rotational motion.
is in a translational motion.
The correct Answer is:A, B, C, D
To solve the question, we need to understand the relationship between angular momentum, torque, and the center of mass of a system of particles. The question states that the rate of change of angular momentum of a system of particles about the center of mass is equal to the sum of external torque about the center of mass when the center of mass is in a specific condition.
1. Understanding Angular Momentum and Torque:
- The angular momentum L of a system of particles about a point (in this case, the center of mass) is defined as:
L=r×p
where r is the position vector from the center of mass to the particle, and p is the linear momentum of the particle.
2. Rate of Change of Angular Momentum:
- The rate of change of angular momentum with respect to time is given by:
dLdt=τnet
where τnet is the net external torque acting on the system about the center of mass.
3. Condition for the Center of Mass:
- The equation dLdt=τnet holds true when the center of mass is in a specific frame of reference. This frame is typically an inertial frame, where Newton's laws of motion are valid.
4. Inertial Frame:
- An inertial frame is one that is either at rest or moving at a constant velocity. In such frames, the laws of physics, including the conservation of momentum and angular momentum, apply without the influence of fictitious forces.
5. Conclusion:
- Therefore, the rate of change of angular momentum of a system of particles about the center of mass is equal to the sum of external torque about the center of mass when the center of mass is fixed with respect to an inertial frame.
Final Answer:
The rate of change of angular momentum of a system of particles about the center of mass is equal to the sum of external torque about the center of mass when the center of mass is fixed with respect to an inertial frame.
---
- The angular momentum L of a system of particles about a point (in this case, the center of mass) is defined as:
L=r×p
where r is the position vector from the center of mass to the particle, and p is the linear momentum of the particle.
- The rate of change of angular momentum with respect to time is given by:
dLdt=τnet
where τnet is the net external torque acting on the system about the center of mass.
- The equation dLdt=τnet holds true when the center of mass is in a specific frame of reference. This frame is typically an inertial frame, where Newton's laws of motion are valid.
- An inertial frame is one that is either at rest or moving at a constant velocity. In such frames, the laws of physics, including the conservation of momentum and angular momentum, apply without the influence of fictitious forces.
- Therefore, the rate of change of angular momentum of a system of particles about the center of mass is equal to the sum of external torque about the center of mass when the center of mass is fixed with respect to an inertial frame.
The rate of change of angular momentum of a system of particles about the center of mass is equal to the sum of external torque about the center of mass when the center of mass is fixed with respect to an inertial frame.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 88
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:Now answer the following :
Explore 20 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 86
Explore 6 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 53 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
The momentum of a system with respect to centre of mass
View Solution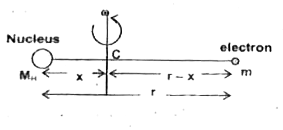
The angular momentum of the atom about the centre of mass will be
View SolutionThe torque on a planet about the centre of sun is
View SolutionCalculate centre of mass of the system
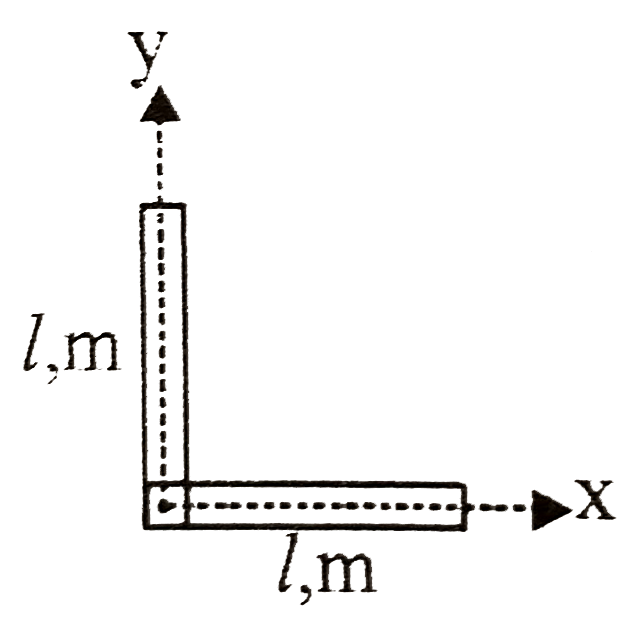
View SolutionThe centre of mass of a system of particles is at the origin. It follows that:
View SolutionIf the external forces acting on a system have zero resultant, the centre of mass
View SolutionIf all the particle of a system lie in a cube is it necessary that the centre of mass be in the cube?
View SolutionThe position of centre of mass of system of particles at any moment does not depend on.
View SolutionIn a binary star system one star has thrice the mass of other. The stars rotate about their common centre of mass then :
View SolutionWhat is the difference between centre of mass and centre of gravity?
View Solution

