A solid sphere of mass m and radiusr is given an initial angular velocity ω0 and a linear velocity v0=λrω0 from a point A on a rough horizontal surface .It is observed that the ball turns back and returens to the point A after some time if λ is less than a certain maximum value λ0 . Find λ0.
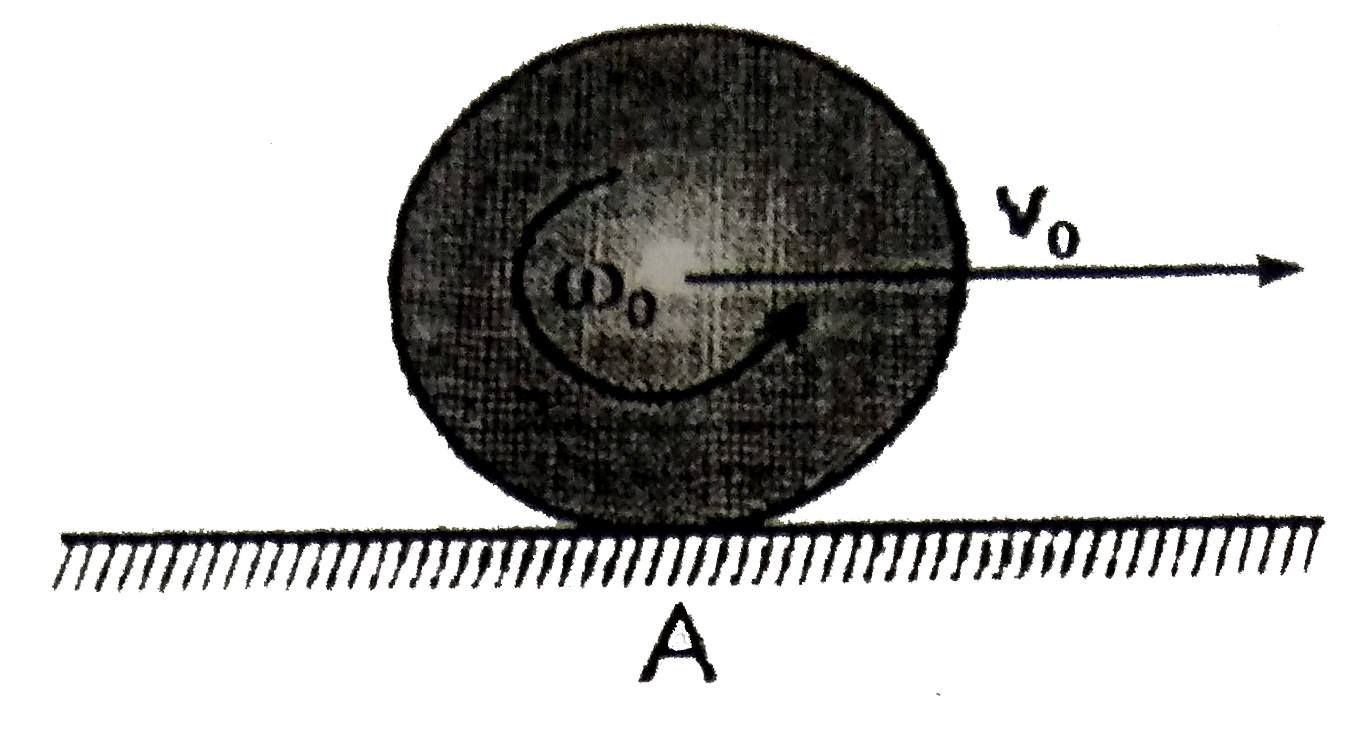
The correct Answer is:λ0=2/5
Ball will comes back to the initial position if its angular velocity is greater than zero is the same direction (in which it was released) at the moment its's linear velocity becomes zero. In his condition ball would returen back.

0=v0+(μg)t
t=v0μg (time when ball stop)
For rotation motion

τ=Iα
⇒α=τI=μgm×R¯¯¯¯¯¯¯¯¯¯¯¯25MR2=5μg2R2
using ωf=ω0−αt
ωf>0
⇒v0αR>5μg2R.v0μg for limiting condition
⇒λ0=25
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 67
Explore 2 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 68
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:DPP 65
Explore 5 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 53 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
A disc is given an angular velocity ω0 and a linear velocity v0 as shown in the figure. It is released on a rough horizontal surface of friction coefficient μ. Mark the correct statement (ω0=3v0/R)

View SolutionA disc is given an initial angular velocity ω0 and placed on a rough horizontal surface as shown Fig. The quantities which will not depend on the coefficient of friction is/are

View SolutionA uniform solid sphere of mass m and radius 'R' is imparted an initial velocity v0 and angular ω0=2v0R and then placed on a rough inclined plane of inclination 'theta' and coefficient of friction μ=2tanθ as shown. The time after which the sphere will start rolling without slipping is

View SolutionA solid sphere of mass M is placed on the top of a plank of the same mass, after giving an angular velocity ω0 at t=0. Find the velocity of the plank and the sphere when the sphere starts rolling:,

View Solution_S01_038_Q01.png)
As per the shown figure the central solid cylinder starts with initial angular velocity ω0 Find the time after which the angular velocity becomes half.
View SolutionA disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View SolutionA uniform sphere of radius R is palced on a rough horizontal surface and given a linear velocity v0 and an angular velocity ω0 as shown . If the angular velocity and the linear velocity both become zero simultaneously, then
View SolutionA hoop of radius r mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it cases to slip ?
View SolutionA solid sphere of mass M and radius R is in pure rolling as shown in figure. The angular momentum of the sphere about the origin is (linear velocity of centre of mass is v0, in positive x-direction)
View SolutionA sphere of mass m is placed on a rough surface of coefficient of friction μ. Initially the sphere is given a velocity v0 and angular velocity ω0 as shown in figure. Find out the value of ω0 so that the sphere will come to rest after a certain time. Sphere has radius r.

View Solution