The end 'A' of a uniform rod AB of length 'l' touches a horizontal smooth fixed surface. Initially the rod makes an angle of 30∘ with the vertical. Find the magnitude of displacement of the end B just before it touches the ground after the rod is released.
The correct Answer is:√13l4
To solve the problem of finding the magnitude of displacement of the end B of the rod just before it touches the ground, we can follow these steps:
Step 1: Understand the Initial Setup
The rod AB has a length l and initially makes an angle of 30∘ with the vertical. This means that the angle with the horizontal is 60∘.
Step 2: Identify the Positions of Points A and B
- Point A is on the ground (the fixed surface).
- Point B is initially at a height above the ground.
Step 3: Calculate the Initial Height of Point B
The height of point B from the ground can be calculated using trigonometry:
h=l⋅cos(30∘)=l⋅√32
Step 4: Determine the Final Position of Point A
When the rod is released, point A will move horizontally to the left as the rod falls. The final position of point A (let's call it A′) will still be on the ground.
Step 5: Calculate the Final Position of Point B
As the rod falls, point B will move vertically downwards until it touches the ground. The vertical distance it will fall is equal to the initial height h.
Step 6: Calculate the Horizontal Displacement of Point A
Since point A moves horizontally, the horizontal distance that point A moves can be calculated using the length of the rod and the angle:
d=l⋅sin(30∘)=l⋅12
Step 7: Determine the Final Position of Point B
At the moment just before B touches the ground, point B will have moved down by a distance h and point A will have moved left by a distance d.
Step 8: Use the Pythagorean Theorem to Find the Displacement of B
The total displacement of point B can be found using the Pythagorean theorem:
Displacement=√(l⋅12)2+(l⋅√32)2
=
⎷(l2)2+(l⋅√32)2
=√l24+3l24=√4l24=√l2=l
Step 9: Conclusion
Thus, the magnitude of displacement of the end B just before it touches the ground is:
Displacement=l
The rod AB has a length l and initially makes an angle of 30∘ with the vertical. This means that the angle with the horizontal is 60∘.
- Point A is on the ground (the fixed surface).
- Point B is initially at a height above the ground.
The height of point B from the ground can be calculated using trigonometry:
h=l⋅cos(30∘)=l⋅√32
When the rod is released, point A will move horizontally to the left as the rod falls. The final position of point A (let's call it A′) will still be on the ground.
As the rod falls, point B will move vertically downwards until it touches the ground. The vertical distance it will fall is equal to the initial height h.
Since point A moves horizontally, the horizontal distance that point A moves can be calculated using the length of the rod and the angle:
d=l⋅sin(30∘)=l⋅12
At the moment just before B touches the ground, point B will have moved down by a distance h and point A will have moved left by a distance d.
The total displacement of point B can be found using the Pythagorean theorem:
Displacement=√(l⋅12)2+(l⋅√32)2
=
⎷(l2)2+(l⋅√32)2
=√l24+3l24=√4l24=√l2=l
Thus, the magnitude of displacement of the end B just before it touches the ground is:
Displacement=l
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 54
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 55
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 52
7 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A uniform rod is lying against a smooth wall and on a smooth floor. It is relased from rest when it makes an angle θ0 with the ground. Find the angle rod will make with the ground it just leaves the contact with the walls.

View SolutionA conducting rod AB of lemgth 2 l moves through a uniform magnetic field B. The rod makes an angle θ with the vertical while it falls with a uniform linear velocity v. The potential difference between the two ends of the rod is Bv2l .

View SolutionA uniform slender rod of mass m and length L is released from rest, with its lower end touching a frictionaless horizontal floor. At the initial moment, the rod is inclined at an angle θ=30∘ with the vertical. Thent he value of normal reaction from the from the floor just after release will be
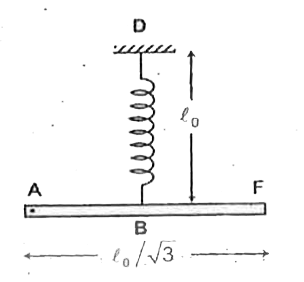
View SolutionIn the figure shown one end of a light spring of natural length l0=√58m(≈0.8m) is fixed at point D and other end is attached to the centre B of a uniform rod AF of length l0/√3 and mass 10kg. The rod is free to rotate in a vertical plane about a fixed horizontal axis passing through the end A of the rod. The rod is held at rest in horizontal position and the spring is in relaxed state. It is found that, when the rod is released to move it makes an angle of 60∘ with the horizontal when it comes to rest for the first time. Find the
(a) the maximum elogation in the spring . (Approximately)
(b) the spring constant. (Approximately)
View SolutionA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:

View SolutionA uniform rod is placed vertically on a smooth surface and then released . Then,
View SolutionA rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.

View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View SolutionA uniform slender rod of mass m and length L is released from rest, with its lower end touching a frictionaless horizontal floor. At the initial moment, the rod is inclined at an angle θ=30∘ with the vertical. Thent he value of normal reaction from the from the floor just after release will be 4mg /7 In the above problem, the initial acceleration of the lower end of the rod will be
View Solution
