Two blocks A and B of mass m and 2m are connected by a massless spring of force constant k . They are placed on a smooth horizontal plane . Spring is stretched by an amount x and then released . The relative velocity of the blocks when the spring comes to its natural length is
The correct Answer is:14kx20
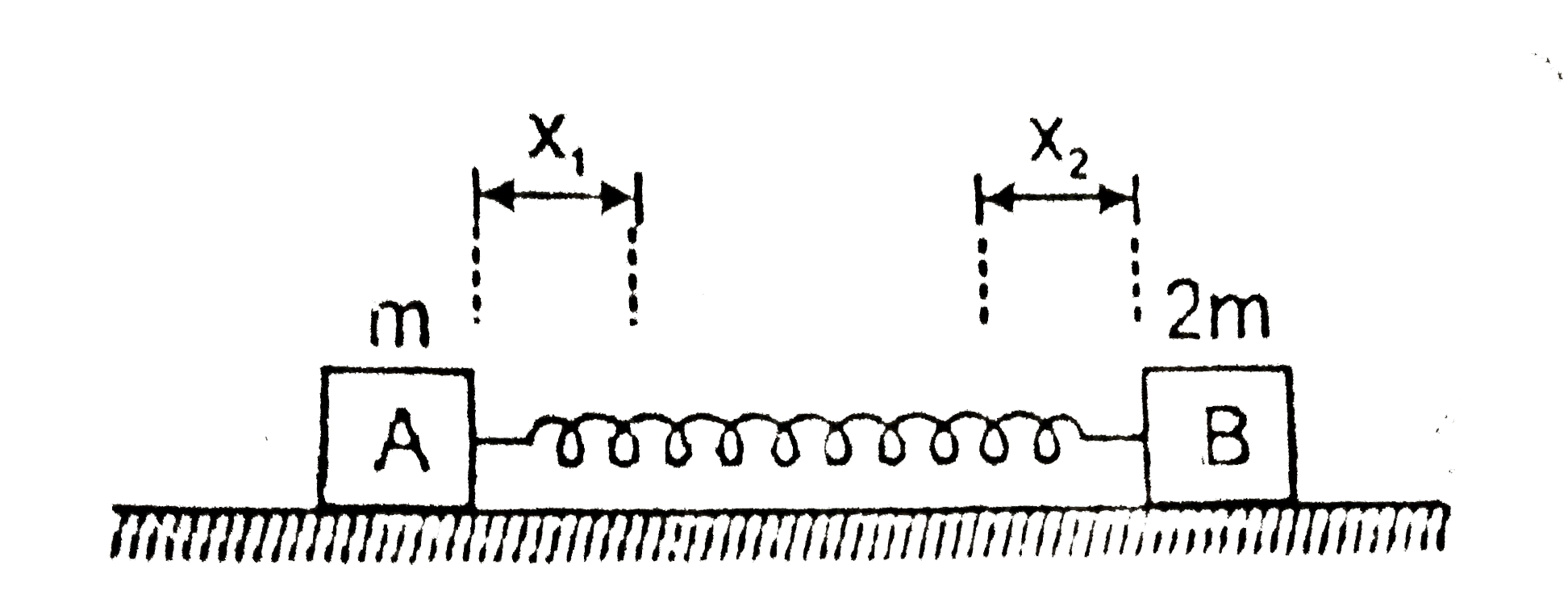
Let the block A shift to left by x1 and block B shift to right by x2. The centre of mass of the two block system is at rest.
Hence mx1=2ms2.
or x2=x12…..(1)
and the spring force on either block is k(x0−[x1+x2]), where x0 is the initial compression in the spring.
Let the block A shift further left by dx1
∴work donw on block by spring is
dW=(k(x0−x1−x2)dx1.....(2)
=k(x0−x1−x12)dx1
∴Net work done
∫dW=x0/3∫x1=0k(x0−32x1)dx1=kx204
Ans.12kx20
Alternative Solution
Let the speeds of blocks A and B at the instant compression is x02 be vA andvB as shown in figure
[l0] natural length of spring ]

No external forces act on the system in the horizontal direction
Applying conservation of momentum in horizontal direction
Initial momentum = final momentum
0=m(−vA)+2mvB
or vA=2vB......(1)
from conservation of energy
12kx20=12k(x02)2+12mv2A+122mv2B....(2)
from (1) and (2) we get
12mv2A=14kx20
work done on block A by spring = change in kinetic energy of block A
=12mv2A=14kx20
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 53
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 54
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 51
7 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Two blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionTwo blocks A and B of masses 3 kg and 6 kg are connected by a massless spring of force constant 1800 N m−1 and then they are placed on a smooth horizontal surface. The blocks are pulled apart to stretch the spring by 5 cm and then released. What is the relative velocity (in ms−1) of the blocks when the spring comes to its natural length?
View SolutionTwo blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.

What is acceleration of centre of mass of system at the instant of maximum elongation of spring
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.
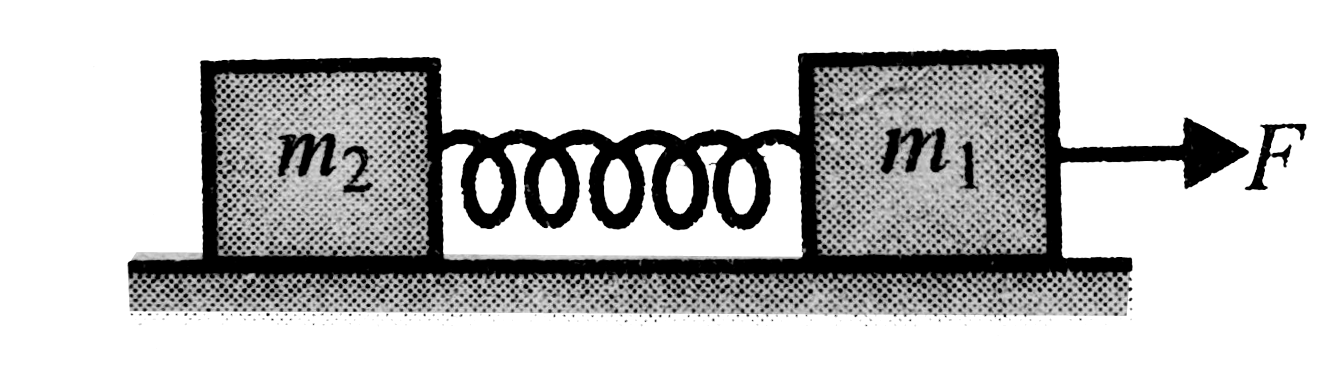
Which of the following statement is not true tn the watt of above system.
View SolutionTwo blocks of masses m1 and m2, connected by a weightless spring of stiffness k rest on a smooth horizontal plane as shown in Fig. Block 2 is shifted a small distance x to the left and then released. Find the velocity of centre of mass of the system after block 1 breaks off the wall.

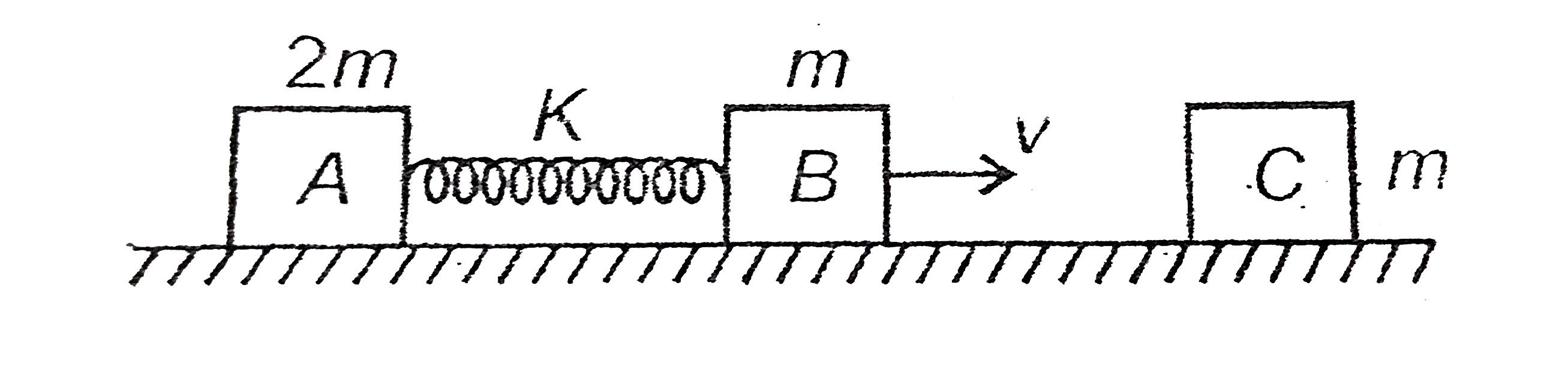
View SolutionTwo blocks A and B of mass 2m and m respectively are connected to a massless spring of force constant K as shown in figure A and B are moving on the horizontal frcitionless surface with velocity v to right with underformed spring. If B collides with C elastically, then maximum compression of the spring will be
View SolutionTwo identical blocks A and B of mass m each are connected to each other by spring of spring constant k. Block B is initially shifted to a small distance x0 to the left and then released. Choose the correct statements for this problem, after the spring attains it's natural length.
View SolutionA block of mass m is connected to another block of mass M by a massless spring of spring constant k. the blocks are kept of a smooth horizontal plane and are at rest. The spring is unstretched when a constant force F starts acting on the block of mass M of pull it. Find the maximum extension of the spring
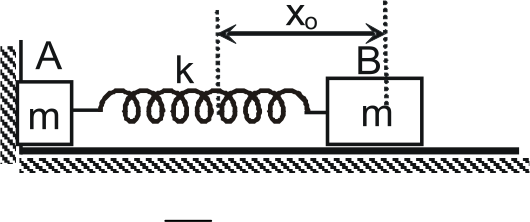
View SolutionTwo blocks A and B of mass m and 2m are connected together by a light spring of stiffness k. The system is lying on a smooth horizontal surface with block A in contact with a fixed vertical wall as shown in the figure. The block B is pressed towards the wall by a distance x0 and then released. There is not friction anywhere. If spring takes time Δt to aquire its natural length then average force on the block A by the wall is

View Solution
