A particle of mass m initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B.C is centre of the hemisphere. The equation relating θ and θ' is
 .
.
3sinα=2cosβ
2sinα=3cosβ
3sinβ=2cosα
2sinβ=3cosα
The correct Answer is:C
(C) Let v be the speed of particle at B, just when it is about to loose contact.
From application of Newton's second law to the particle normal to the spherical surface.
mv2r=mgsinβ....(1)
Applying conservation of energy as the block moves from A to B.
12mv2=mg(rcosα−rsinβ)....(2)
Solving 1 and 2 we get
3sinβ=2cosα
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 44
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:DPP 45
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 42
Explore 7 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 53 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
A small block of mass m has speed√gR2 at the top most point of a fixed hemisphere of radius R as shown in figure. The angle θ, when block loses the contact with the hemisphere is
_PHY_E05_149_Q01.png)
View SolutionA particle of mass m is placed in equilibrium at the top of a fixed rough hemisphere of radius R. Now the particle leaves the contact with the surface of the hemisphere at angular position θ with the vertical where cosθ=35. if the work done against friction is 2mgR10x, find x.
View SolutionA partical moves from rest at A on the surface of a smooth circule cylinder of radius r as shown . At B it leavels the cylinder. The equation releaseder . The equation relating αandβ is

View SolutionA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.

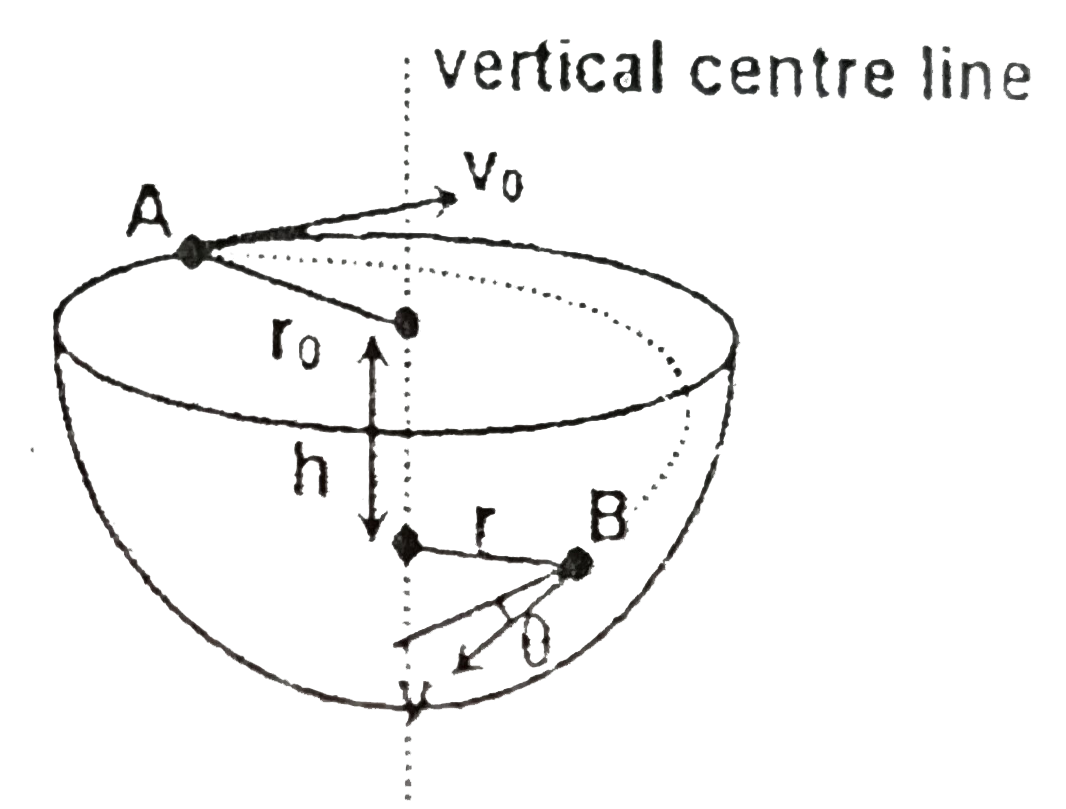
View SolutionA small particle is given an initial velocity v0=10m/s along the tangent to the brim of a fixed smooth hemisphere bowl of radius r0=15√2m as shown in the figure. The particle slides on the inner surface and reaches point B, a vertical distance h=15m below A and a distance r from the vertical centerline, where its velocity v makes an angle θ with the horizontal tangent to the bowl through B. If θ=15K∘. Find the value of K. (take g=10m/s2)
View SolutionA particle of mass m is projected with speed √Rg4 from top of a smooth hemisphere as shown in figure. If the particle starts slipping from the highest point, then the horizontal distance between the point where it leaves contact with sphere and the point at which the body was placed is
View SolutionA small solid sphere of mass m and radius r starting from rest from the rim of a fixed hemispherical bowl of radius R(>>r) rolls inside it without sliding. The normal reaction exerted by the sphere on the hemisphere when it reaches the bottom of hemisphere is

View SolutionA paraxial beam is incident on a glass (n=1.5) hemisphere of radius R=6 cm in air as shown. The distance of point convergence F from the plane surface of hemisphere is :-
_E01_026_Q01.png)
View SolutionA point particle of mass m is released from a distance √3R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.

View SolutionA particle of mass m was transferred from the centre of the base of a uniform hemisphere of mass M and radius R into infinity.
What work was performed in the process by the gravitational force exerted on the particle by the hemisphere?
View Solution