Two cars A andB are racing along straight line. Car A is leading, such that their relative velocity is directly proportional to the distance between the two cars. When the lead of car A is l1=10m , its running 10m/s faster than car B. Determine the time car A will take to increase its lead to l2=20m from car B.
The correct Answer is:t=(loge2)sec
To solve the problem, we need to analyze the relationship between the velocities of the two cars and the distance between them. Let's break it down step by step.
Step 1: Understand the relationship between relative velocity and distance
We are given that the relative velocity of car A with respect to car B is directly proportional to the distance between them. Mathematically, this can be expressed as:
vA−vB=k⋅(xA−xB)
where vA is the velocity of car A, vB is the velocity of car B, xA is the position of car A, xB is the position of car B, and k is a proportionality constant.
Step 2: Set up the initial conditions
From the problem, we know:
- When the lead l1=10m, the relative velocity vA−vB=10m/s.
- Thus, we can write:
10=k⋅10
From this, we can solve for k:
k=1
Step 3: Write the equation for relative velocity
Now we can rewrite the equation for relative velocity:
vA−vB=(xA−xB)
This tells us that the difference in velocities is equal to the distance between the two cars.
Step 4: Define the distance variable
Let y=xA−xB. Therefore, we can express the equation as:
dydt=y
Step 5: Separate variables and integrate
We can separate the variables:
dyy=dt
Now we integrate both sides. The limits for y will change from 10m to 20m and for t from 0 to T:
∫20101ydy=∫T01dt
Step 6: Perform the integration
The left side integrates to:
ln(y)∣∣∣2010=ln(20)−ln(10)=ln(2010)=ln(2)
The right side integrates to:
T−0=T
Step 7: Set the equations equal
Now we can set the two sides equal:
ln(2)=T
Step 8: Calculate the time T
Using the value of ln(2):
T≈0.693s
Final Answer
The time car A will take to increase its lead from 10 m to 20 m is approximately 0.693s.
---
We are given that the relative velocity of car A with respect to car B is directly proportional to the distance between them. Mathematically, this can be expressed as:
vA−vB=k⋅(xA−xB)
where vA is the velocity of car A, vB is the velocity of car B, xA is the position of car A, xB is the position of car B, and k is a proportionality constant.
From the problem, we know:
- When the lead l1=10m, the relative velocity vA−vB=10m/s.
- Thus, we can write:
10=k⋅10
From this, we can solve for k:
k=1
Now we can rewrite the equation for relative velocity:
vA−vB=(xA−xB)
This tells us that the difference in velocities is equal to the distance between the two cars.
Let y=xA−xB. Therefore, we can express the equation as:
dydt=y
We can separate the variables:
dyy=dt
Now we integrate both sides. The limits for y will change from 10m to 20m and for t from 0 to T:
∫20101ydy=∫T01dt
The left side integrates to:
ln(y)∣∣∣2010=ln(20)−ln(10)=ln(2010)=ln(2)
The right side integrates to:
T−0=T
Now we can set the two sides equal:
ln(2)=T
Using the value of ln(2):
T≈0.693s
The time car A will take to increase its lead from 10 m to 20 m is approximately 0.693s.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 20
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 21
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 18
7 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Two cars A and B are moving on parallel roads in the same direction. Car A moves with constant velocity 30m/s and car B moves with constant acceleration 2.5m/s2 . At , car A is ahead of car B and car B is moving with 12m/s velocity . The distance travelled by car B until it overtakes car A is
View SolutionA car travels from A to B and returns to its original position.
The distance between A and B is 2000 m.
Find the total displacement of the car.
View Solution
Knowledge Check
two car A and B are moving with velocities of 60kmh−1and45kmh−1 respectively. Calculate the relative velocity of A w.r.t B if (i) both cars are travelling eastwards and (ii)car A is travelling eastwards and car B is travelling westwards.
A15kmh−1B45kmh−1C60kmh−1D105kmh−1
A car of mass m is driven with acceleration a along a straight level road against a constant external resistive force R. When the velocity of the car V, the rate at which the engine of the car is doing work will be
View SolutionA car of mass m is driven with acceleration a along a straight level road against a constant external resistive force R. When the velocity of the car V, the rate at which the engine of the car is doing work will be
View SolutionTwo cars A and B start moving from the same point with same velocity v=5km/minute. Car A moves towards North and car B in moving towards East. What is the relative velocity of B with respect to A ?
View SolutionTwo cars A and B are moving in same direction with velocities 30 m/s and 20 m/s. When car A is at a distance d behind the car B, the driver of the car A applies brakes producing uniform retardation of 2m/s2. There will be no collision when :-
View SolutionCar A and car B move on a straight road and their velocity versus time graph are as shown in figure. Comparing the motion or car A in between t=0 to t=8sec. And motion of car B in between t=0 to t=7sec., pick up the correct statement.
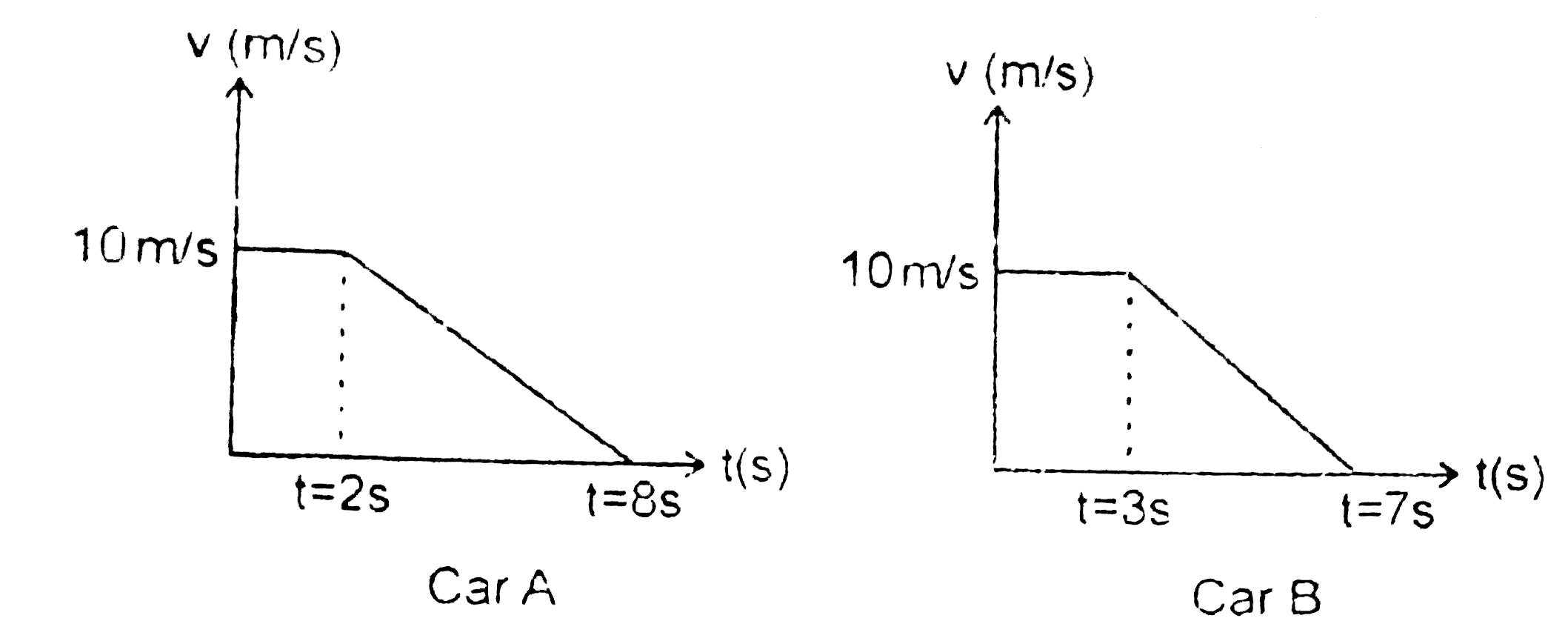 .
.
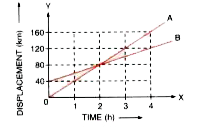
View SolutionFig. 2.40 ahead represents the displacement-time sketch of motion of two cars A and B. Find :(i) the distance by which the car B was initially ahead of car A.
(ii) the velocities of car A and car B.
(iii) the time in which car A catches car B.
(iv) the distance from start when the car A will catch the car B.
View SolutionTwo cars A and B cross a point P with velocities 10m/s and 15m/s. After that they move with different uniform accelerations and the car A overtakes B with a speed of 25ms−1. What is velocity of B at that instant?
View Solution
