A stone is dropped from the top of a tower. When it crosses a point 5 m below the top, another stone is let fall from a point 25 m below the top. Both stones reach the bottom of the tower simultaneously. Find the height of the tower. Take g=10m/s2.
45m
50m
60m
65m
The correct Answer is:A
Vel. Of 1st stone when passing at A→
V2=0+2.10.5
S1−S2=20m.
⇒(10.t+1210.t2)−(12.10.t2)=20
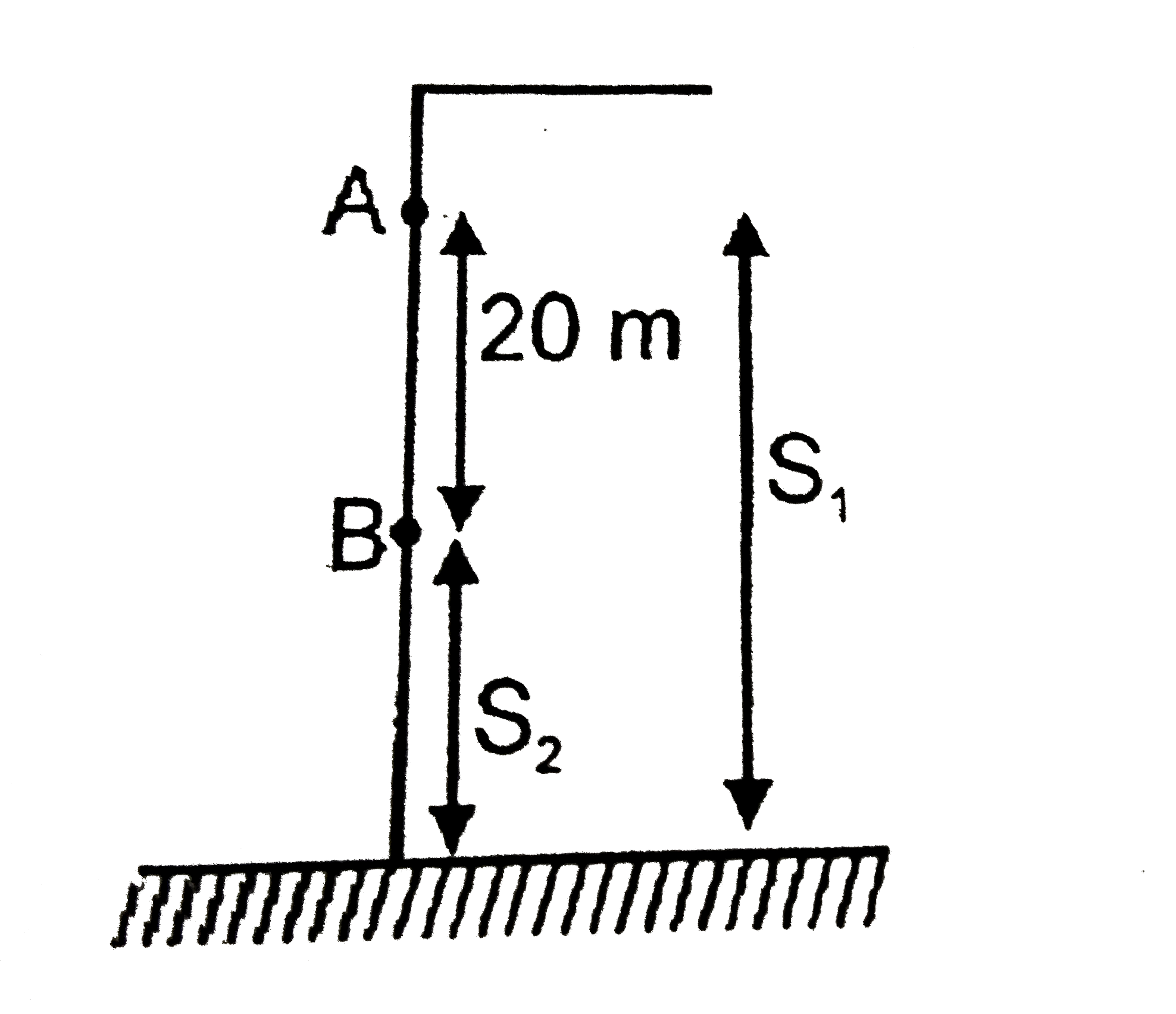
t=2s
S2=12.10.4=20m
Ht=25+20=45m.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 15
Explore 8 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 16 physics
Explore 8 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:Dpp no. 13 physics
Explore 5 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 53 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
A stone is dropped from the top of tower. When it has fallen by 5m from the top, another stone is dropped from a point 25m below the top. If both stones reach the ground at the moment, then height of the tower from grounds is : (take g=10m/s2)
View SolutionA stone is dropped from the top of a tower of height h. Aftre 1s another stone is droppped from the balcony 20m below the top. Both reach the bottom simultaneously. What is the value of h ? Take g=10ms−2.
View SolutionA stone dropped from the top of a tower reaches the ground in 3 s. The height of the tower is
View SolutionA particle is dropped from the top of a tower. It covers 40 m in last 2s. Find the height of the tower.
View SolutionA stone is dropped from the top of a tower. If it hits the ground after 10 seconds, what is the height of the tower?
View SolutionA stone is dropped from the top of a tower and travels 24.5 m in the last second of its journey. The height of the tower is
View SolutionA stone is dropped from a hill of height 180 m. Two seconds later another stone is dropped from a point P below the top of the hill . If the two stones reach the groud simultaneously, the height of P from the ground is (g=10ms−2)
View SolutionThe angle elevation of the top of a tower from a point C on the ground. Which is 30 m away from the foot of the tower is 30∘ . Find the height of the tower.

View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 40 m away from the foot of the tower is 30∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30m away from the foot of the tower is 30∘ . Find the height of the tower.
View Solution

