Estimate the temperature at which a body may appear blue or red. The values of λmean for these are 5000 and 7500Å respectively. [Given Wein's constant b=0.3cmK]
The correct Answer is:6×103K;4×103K
To estimate the temperature at which a body may appear blue or red, we can use Wien's Displacement Law, which states that the wavelength at which the emission of a black body spectrum is maximized (λ_max) is inversely proportional to the temperature (T) of the body. The formula is given by:
λmax=bT
where b is Wien's constant.
1. Identify Given Values:
- For blue light: λblue=5000Å=5000×10−10m=5×10−7m
- For red light: λred=7500Å=7500×10−10m=7.5×10−7m
- Wien's constant b=0.3cm⋅K=0.3×10−2m⋅K
2. Calculate Temperature for Blue Light:
- Using the formula, rearrange to find T:
Tblue=bλblue
- Substitute the values:
Tblue=0.3×10−25×10−7=0.3×10−25×10−7=6000K
3. Calculate Temperature for Red Light:
- Similarly, use the formula for red light:
Tred=bλred
- Substitute the values:
Tred=0.3×10−27.5×10−7=0.3×10−27.5×10−7=4000K
4. Final Results:
- The temperature at which a body may appear blue is approximately 6000 K.
- The temperature at which a body may appear red is approximately 4000 K.
Summary of Results:
- Temperature for blue light: 6000 K
- Temperature for red light: 4000 K
- For blue light: λblue=5000Å=5000×10−10m=5×10−7m
- For red light: λred=7500Å=7500×10−10m=7.5×10−7m
- Wien's constant b=0.3cm⋅K=0.3×10−2m⋅K
- Using the formula, rearrange to find T:
Tblue=bλblue
- Substitute the values:
Tblue=0.3×10−25×10−7=0.3×10−25×10−7=6000K
- Similarly, use the formula for red light:
Tred=bλred
- Substitute the values:
Tred=0.3×10−27.5×10−7=0.3×10−27.5×10−7=4000K
- The temperature at which a body may appear blue is approximately 6000 K.
- The temperature at which a body may appear red is approximately 4000 K.
- Temperature for blue light: 6000 K
- Temperature for red light: 4000 K
Topper's Solved these Questions
- HEAT TRANSFERBook:RESONANCE ENGLISHChapter:HEAT TRANSFERExercise:Exercise-2
Explore 1 Video
- HEAT TRANSFERBook:RESONANCE ENGLISHChapter:HEAT TRANSFERExercise:Exercise-3
Explore 1 Video
- HEAT TRANSFERBook:RESONANCE ENGLISHChapter:HEAT TRANSFERExercise:Exercise-1
Explore 1 Video
- GRAVITATIONBook:RESONANCE ENGLISHChapter:GRAVITATIONExercise:Exercise
Explore 21 Videos
- KINEMATICSBook:RESONANCE ENGLISHChapter:KINEMATICSExercise:Exercise
Explore 65 Videos
Similar Questions
Calculate the temperature at which a body may appear (i) deep red (7900A) and (ii) blue (5000A).
View Solution(a) Write the approximate wavelength for (i) blue, and (ii) red light
(b) The wavelength of violet and red light are 4000Å and 8000Å respectively. Which of the two has higher frequency?
View Solution
Knowledge Check
Experimental investigations show that the intensity of solar radiation is maximum for a wavelength 480nm in the visible ragion. Estimate the surface temperature of sun. (Given Wien's constant b=2.88×10−3mK).
A4000KB6000KC8000KD106K
Two bodies A and B have emissivities 0.5 and 0.8 respectively. At some temperature the two bodies have maximum spectral emissive powers at wavelength 8000Å and 4000Å respectively. The ratio of their emissive powers at these temperatures is :
View SolutionThe surface temperature of a hot body is 1227∘C. Find the wavelength at which it radiates maximum energy. Given Wien's constant = 0.2892 cm.K.
View SolutionBoyle's temperature (TB) : It is the temperature at which a real gas exhibits ideal behavior in low pressure range. Different gases have different value of TB, which is related to the van der Wall's constant a and ab as follows: TB=aRb
The compressiblity factor for a real gas is given as Z=1+0.35P−168TP. Where P is in bar and T is in Kelvin. What is the Boyle's temperature of the gas?
View SolutionThe temperature at which the root mean squres speed of a gas will be half its value at 0∘C is (assume the pressure remains constant)
View SolutionN2 and O2 combine at a given temperature to produce NO. At equilibrium the yield of NO is 'x' precent by volume. If x=√Ka.b−K(a+b)4, where K is the equilibrium constant of the given reaction at the given temperature and a and b are the volume percentage of N2 and O2, respectively, in the initial state. Report. Report the value of K at which X is maximum
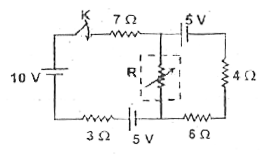
View SolutionIn the circuit shown the resistance R is kept in a chamber whose temperature. is 20∘C which remains constant. The initial temperature and resistance of R is 50∘C and 15Ωrespectively. The rate of change of resistance R with temperature is 12Ω/∘C and the rate of decrease of temperature of R is In(3/100) times the temperature difference from the surrounding (Assume the resistance R loses heat only in accordance with Newton's law of cooling) If K is closed at t = 0, then find the
(a) value of. R for which power dissipation in it is maximum.
(b) temperature of R when power dissipation is maximum
(c) time after which the power dissipation will be maximum
View SolutionIn the given pressure - temperature (P-T) diagram, the density of an ideal gas at point A and B are ρ0 and 3ρ02respectively, then the value of X is
View Solution

