The energy levels in a certain single electron species are all 800% higher in magnitude than corresponding levels of atomic hydrogen. A certain transition of the electron from the nth excited state to the next higher level is possible with a photonn of wavelength 72nm. Find the value of n .
Given : (1R=90nm)
The correct Answer is:1
To solve the problem, we will follow these steps:
Step 1: Understand the Energy Levels
The energy levels of a hydrogen atom are given by the formula:
En=−Rn2
where R is the Rydberg constant. In this case, the energy levels of the given single electron species are 800% higher in magnitude than those of hydrogen. This means that the energy levels can be expressed as:
E′n=−R′n2
where R′=9R (since 800% higher means 9 times the energy).
Step 2: Use the Rydberg Formula
The Rydberg formula for the wavelength of emitted or absorbed light during a transition between two energy levels is given by:
1λ=R′(1n21−1n22)
Here, λ=72nm and R′=190nm.
Step 3: Substitute Values into the Rydberg Formula
Substituting the values into the Rydberg formula:
172=190(1n21−1n22)
Step 4: Rearranging the Equation
Multiply both sides by 90:
9072=1n21−1n22
This simplifies to:
54=1n21−1n22
Step 5: Identify the Transition
Since the transition is from the nth excited state to the next higher level, we can denote:
- n2=n
- n1=n−1
Substituting these into the equation gives:
54=1(n−1)2−1n2
Step 6: Solve the Equation
To solve the equation, we first find a common denominator:
54=n2−(n−1)2(n−1)2n2
Expanding the numerator:
n2−(n2−2n+1)=2n−1
So we have:
54=2n−1(n−1)2n2
Step 7: Cross Multiply
Cross multiplying gives:
5(n−1)2n2=8n−4
Step 8: Solve for n
This is a quadratic equation in n. After simplifying and solving, we find that n=2.
Conclusion
Thus, the value of n is:
2
The energy levels of a hydrogen atom are given by the formula:
En=−Rn2
where R is the Rydberg constant. In this case, the energy levels of the given single electron species are 800% higher in magnitude than those of hydrogen. This means that the energy levels can be expressed as:
E′n=−R′n2
where R′=9R (since 800% higher means 9 times the energy).
The Rydberg formula for the wavelength of emitted or absorbed light during a transition between two energy levels is given by:
1λ=R′(1n21−1n22)
Here, λ=72nm and R′=190nm.
Substituting the values into the Rydberg formula:
172=190(1n21−1n22)
Multiply both sides by 90:
9072=1n21−1n22
This simplifies to:
54=1n21−1n22
Since the transition is from the nth excited state to the next higher level, we can denote:
- n2=n
- n1=n−1
54=1(n−1)2−1n2
To solve the equation, we first find a common denominator:
54=n2−(n−1)2(n−1)2n2
Expanding the numerator:
n2−(n2−2n+1)=2n−1
So we have:
54=2n−1(n−1)2n2
Cross multiplying gives:
5(n−1)2n2=8n−4
This is a quadratic equation in n. After simplifying and solving, we find that n=2.
Thus, the value of n is:
2
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - III CHEMISTRY
20 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - Chemistry
701 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - III CHEMISTRY SEC - 2
18 Videos
- SURFACE CHEMISTRYBOOK - RESONANCE ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - Section - 5
1 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - CHEMISTRY
50 Videos
Similar Questions
The energy levels of a hypotherical one electron atom are shown in figure
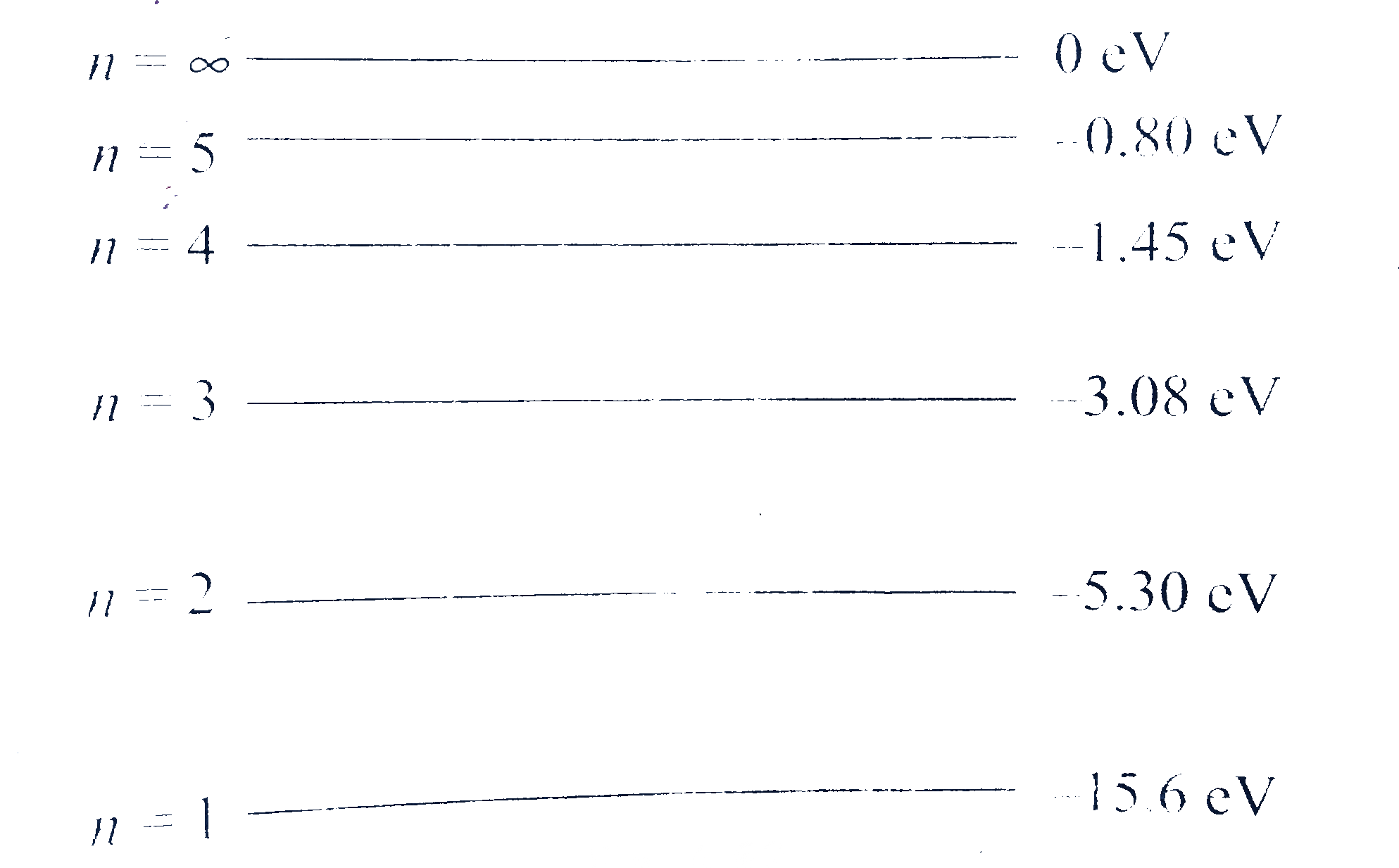
Find the excitation potential for the state n=3.
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure
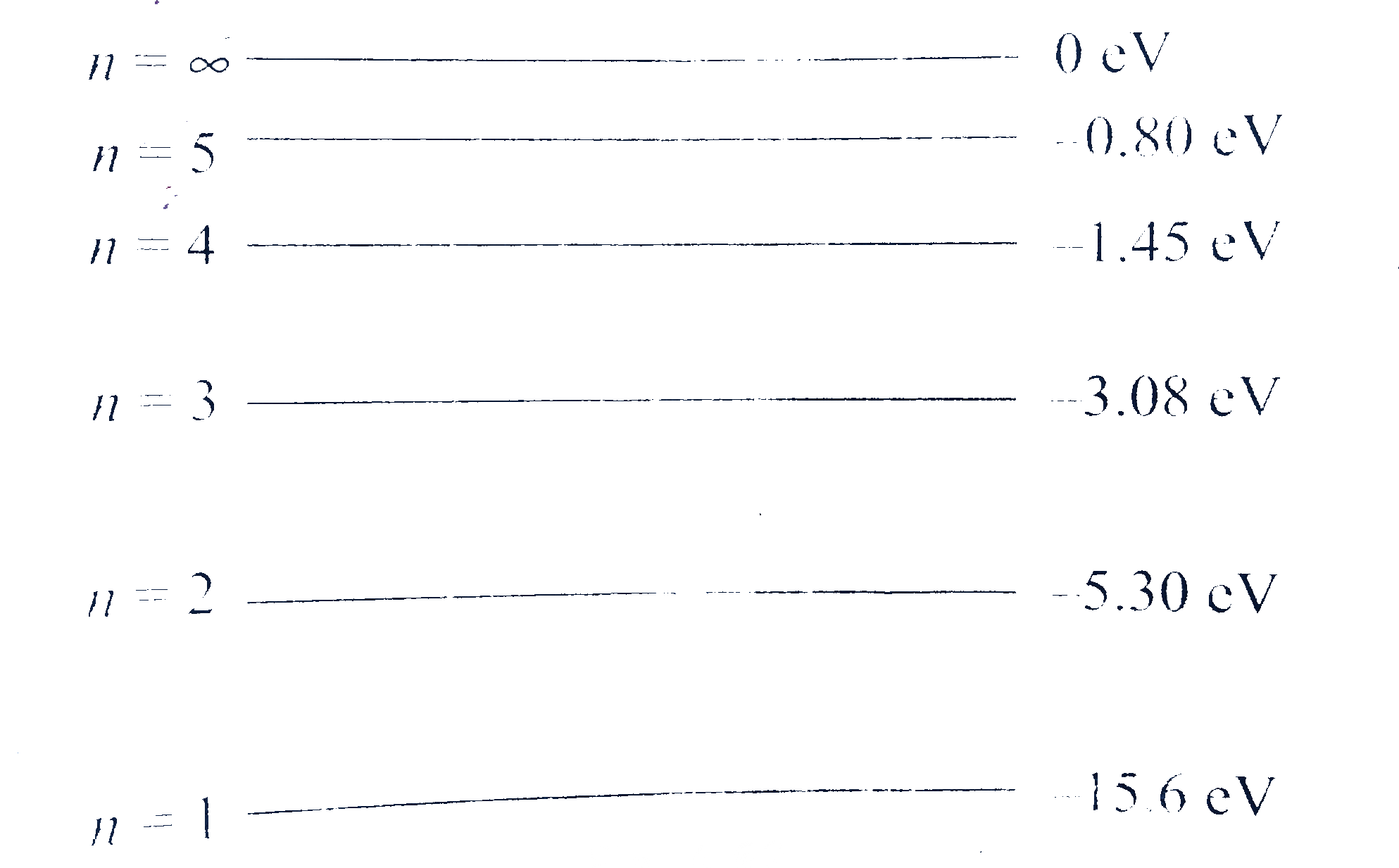
Find the wave number of the photon emitted for the transition n=3→n=1
View SolutionIn a hydrogen (H) sample on excitation electron jumps into nth energy level and comes back to its ground energy level giving 6 different spectrum lines. Determine value of n.
View SolutionWhat is the wavelength of light emitted when the electron in a hydrogen atom undergoes transition from the energy level with n=4 to the energy level with n=1 ?
View SolutionFind the quantum number n corresponding to nth excited state of He++ ion if on transition to the ground state the ion emits two photons in succession with wavelength 108.5 nm and 30.4 nm. The ionization energy of the hydrogen atom is 13.6 eV.
View SolutionWhat is the wavelength of light emitted when the electron of a hydrogen atom undergoes a transition from an energy level with n=4 to an energy level with n=2? .What is the colour corresponding to this wavelength ?
View SolutionIn a hydrogen atom the electron makes a transition from (n+1)th level to thenth level .If n>>1 the frequency of radiation emitted is proportional to :
View SolutionTo which quantum level does the electron jump in H atom from the lowest level if it is given an energy corresponding to 99% of the ionization potential of hydrogen atom?
View SolutionThe electron in a hydrogen atom at rest makes a transition from n=2 energy state to the n=1 ground state.
find the energy (eV) of the emitted photon.
View SolutionCalculate the wavelength of radiation emited when an electron in a hydrogen atom makes a transition from an energy level with n=3 to a level with n=2
View Solution
