The solution set of (x2+x+1)(x2)log(x)(x+1)(x+9)<0 is
(0,1)∪(1,2)
(1,2)
(0,1)
(0,2)
The correct Answer is:C
To solve the inequality
(x2+x+1)(x2logx)(x+1)(x+9)<0,
we will follow these steps:
Step 1: Identify the critical points
The critical points occur when the numerator or denominator is zero.
1. Numerator:
- x2+x+1=0 has no real roots since its discriminant B2−4AC=12−4(1)(1)=1−4=−3<0. Thus, x2+x+1>0 for all x.
- x2logx=0 gives x=0 or logx=0 which gives x=1.
2. Denominator:
- x+1=0 gives x=−1.
- x+9=0 gives x=−9.
Thus, the critical points are x=0, x=1, x=−1, and x=−9.
Step 2: Determine the intervals
The critical points divide the number line into intervals. We will analyze the sign of the expression in each interval. The intervals are:
1. (−∞,−9)
2. (−9,−1)
3. (−1,0)
4. (0,1)
5. (1,∞)
Step 3: Test the sign of the expression in each interval
We will check the sign of the expression in each interval.
1. Interval (−∞,−9): Choose x=−10
- The numerator is positive (since x2+x+1>0 and x2logx is not defined).
- The denominator is negative. Thus, the expression is undefined.
2. Interval (−9,−1): Choose x=−5
- The numerator is positive.
- The denominator is negative. Thus, the expression is negative.
3. Interval (−1,0): Choose x=−0.5
- The numerator is positive.
- The denominator is negative. Thus, the expression is negative.
4. Interval (0,1): Choose x=0.5
- The numerator is positive (since x2+x+1>0 and x2logx<0).
- The denominator is positive. Thus, the expression is negative.
5. Interval (1,∞): Choose x=2
- The numerator is positive.
- The denominator is positive. Thus, the expression is positive.
Step 4: Compile the results
From the testing, we find that the expression is negative in the intervals:
- (−9,−1)
- (−1,0)
- (0,1)
However, since the logarithm is only defined for x>0, we discard the intervals that include negative values.
Final Solution
The solution set for the inequality
(x2+x+1)(x2logx)(x+1)(x+9)<0
is
(0,1).
The critical points occur when the numerator or denominator is zero.
- x2+x+1=0 has no real roots since its discriminant B2−4AC=12−4(1)(1)=1−4=−3<0. Thus, x2+x+1>0 for all x.
- x2logx=0 gives x=0 or logx=0 which gives x=1.
- x+1=0 gives x=−1.
- x+9=0 gives x=−9.
The critical points divide the number line into intervals. We will analyze the sign of the expression in each interval. The intervals are:
2. (−9,−1)
3. (−1,0)
4. (0,1)
5. (1,∞)
We will check the sign of the expression in each interval.
- The numerator is positive (since x2+x+1>0 and x2logx is not defined).
- The denominator is negative. Thus, the expression is undefined.
- The numerator is positive.
- The denominator is negative. Thus, the expression is negative.
- The numerator is positive.
- The denominator is negative. Thus, the expression is negative.
- The numerator is positive (since x2+x+1>0 and x2logx<0).
- The denominator is positive. Thus, the expression is negative.
- The numerator is positive.
- The denominator is positive. Thus, the expression is positive.
From the testing, we find that the expression is negative in the intervals:
- (−1,0)
- (0,1)
The solution set for the inequality
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART : 1MATHEMATICS SEC - 1
1 Video
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART : 1MATHEMATICS
9 Videos
- TEST PAPERBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPEREXERCISE - MATHEMATICS
48 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - MATHEMATICS
132 Videos
Similar Questions
Knowledge Check
The solution set of −223<x+13≤313,x∈R is
A{x:−3<x<3,x∈R}B{x:−3≤x<3,x∈R}C{x:−3≤x≤3,x∈R}D{x:−3<x≤3,x∈R}The solution set of 2x+13<3x−25x∈R on the number line is
A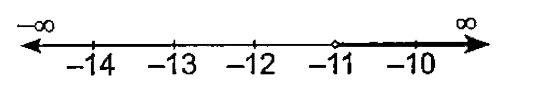 B
B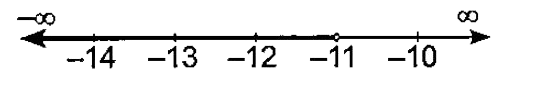 C
C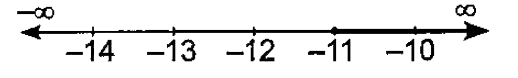 D
D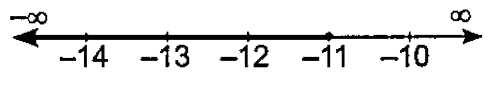
Solution set of (5x−1)<(x+1)2<(7x−3) is
View SolutionThe solution set of the equation 8x=ex2+log(−x) is
View SolutionThe solution set of x2+x+|x|+1<0, is
View SolutionThe solution set of the equation xlogx(1−x)2=9 is
View SolutionThe solution set of (x+1x)2−32(x−1x) =4 when x≠0 is
View SolutionThe solution set of the inequation
log1/3(x2+x+1)+1>0, is
View Solution
