A guard observes an enemy boat, from an observation tower at a height of 180 m above sea level, to be at an angle of depression of 29∘
Calculate, to the nearest metre, the distance of the boat from the foot of the observation tower.
The correct Answer is:325 m (App.)
To solve the problem, we will follow these steps:
Step 1: Understand the Problem
We have a guard observing a boat from a tower that is 180 m high. The angle of depression to the boat is 29 degrees. We need to find the horizontal distance from the base of the tower to the boat.
Step 2: Draw a Diagram
Draw a right triangle where:
- The vertical side (height of the tower) is 180 m.
- The horizontal side (distance from the foot of the tower to the boat) is what we need to find (let's call it x).
- The angle of depression from the top of the tower to the boat is 29 degrees.
Step 3: Relate the Angles
Since the angle of depression from the guard to the boat is 29 degrees, the angle of elevation from the boat to the guard is also 29 degrees (alternate interior angles).
Step 4: Use Trigonometry
We can use the tangent function, which relates the angle of a right triangle to the opposite side and the adjacent side:
tan(θ)=oppositeadjacent
In our case:
tan(29∘)=180x
Step 5: Rearrange the Equation
Rearranging the equation to solve for x:
x=180tan(29∘)
Step 6: Calculate tan(29∘)
Using a calculator, we find:
tan(29∘)≈0.554
Step 7: Substitute and Calculate x
Now substitute the value of tan(29∘) into the equation:
x=1800.554≈324.90
Step 8: Round to the Nearest Metre
Rounding 324.90 to the nearest metre gives us:
x≈325 m
Final Answer
The distance of the boat from the foot of the observation tower is approximately 325 metres.
---
We have a guard observing a boat from a tower that is 180 m high. The angle of depression to the boat is 29 degrees. We need to find the horizontal distance from the base of the tower to the boat.
Draw a right triangle where:
- The vertical side (height of the tower) is 180 m.
- The horizontal side (distance from the foot of the tower to the boat) is what we need to find (let's call it x).
- The angle of depression from the top of the tower to the boat is 29 degrees.
Since the angle of depression from the guard to the boat is 29 degrees, the angle of elevation from the boat to the guard is also 29 degrees (alternate interior angles).
We can use the tangent function, which relates the angle of a right triangle to the opposite side and the adjacent side:
tan(θ)=oppositeadjacent
In our case:
tan(29∘)=180x
Rearranging the equation to solve for x:
x=180tan(29∘)
Using a calculator, we find:
tan(29∘)≈0.554
Now substitute the value of tan(29∘) into the equation:
x=1800.554≈324.90
Rounding 324.90 to the nearest metre gives us:
x≈325 m
The distance of the boat from the foot of the observation tower is approximately 325 metres.
Topper's Solved these Questions
- HEIGHTS AND DISTANCES BOOK - ICSECHAPTER - HEIGHTS AND DISTANCES EXERCISE - Exercise 22 A
14 Videos
- HEIGHTS AND DISTANCES BOOK - ICSECHAPTER - HEIGHTS AND DISTANCES EXERCISE - Exercise 22 B
19 Videos
- GST [GOODS AND SERVICES TAX] BOOK - ICSECHAPTER - GST [GOODS AND SERVICES TAX] EXERCISE - Exercise 1(B)
16 Videos
- LINEAR INEQUATIONSBOOK - ICSECHAPTER - LINEAR INEQUATIONSEXERCISE - Competency Based Questions
15 Videos
Similar Questions
A guard observes an enemy boat, from an observation tower at a height of 180 m above sea level, to be at an angle of depression of 29∘
After some time, it is observed that the boat is 200 m from the foot of the observation tower. Calculate the new angle of depression.
View SolutionFrom the top of a cliff 92 m high. the angle of depression of a buoy is 20∘ . Calculate, to the nearest metre, the distance of the buoy from the foot of the cliff
View SolutionFrom the top of a lighthouse 60 meters high with its base at the sea level, the angle of depression of a boat is 15∘. The distance of the boat from the foot of the lighthouse is
View SolutionForm the top of a light house 60 m high with its base at the sea-level the angle of depression of a boat is 15∘. Find the distance of the boat from the foot of light house.
View SolutionAs observed from the top of a light house, 100m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30o to 45o . Determine the distance travelled by the ship during the period of observation.
View SolutionThe angle of depression of a point situated at a distance of 70 metres from the base of a tower is 45∘. The height of the tower is
View SolutionAn observer on the top of a cliff, 200 m above the sea-level, observes the angles of depression of the two ships to be 45∘and30∘ respectively. Find the distance between the ships, if the ships are
on the same side of the cliff,
View SolutionIn the figure-2, the angle of elevation of the top of tower AC from a point B on the ground is 60∘ . If the height of the tower is 20 m. find the distance of the point from the foot of the tower.
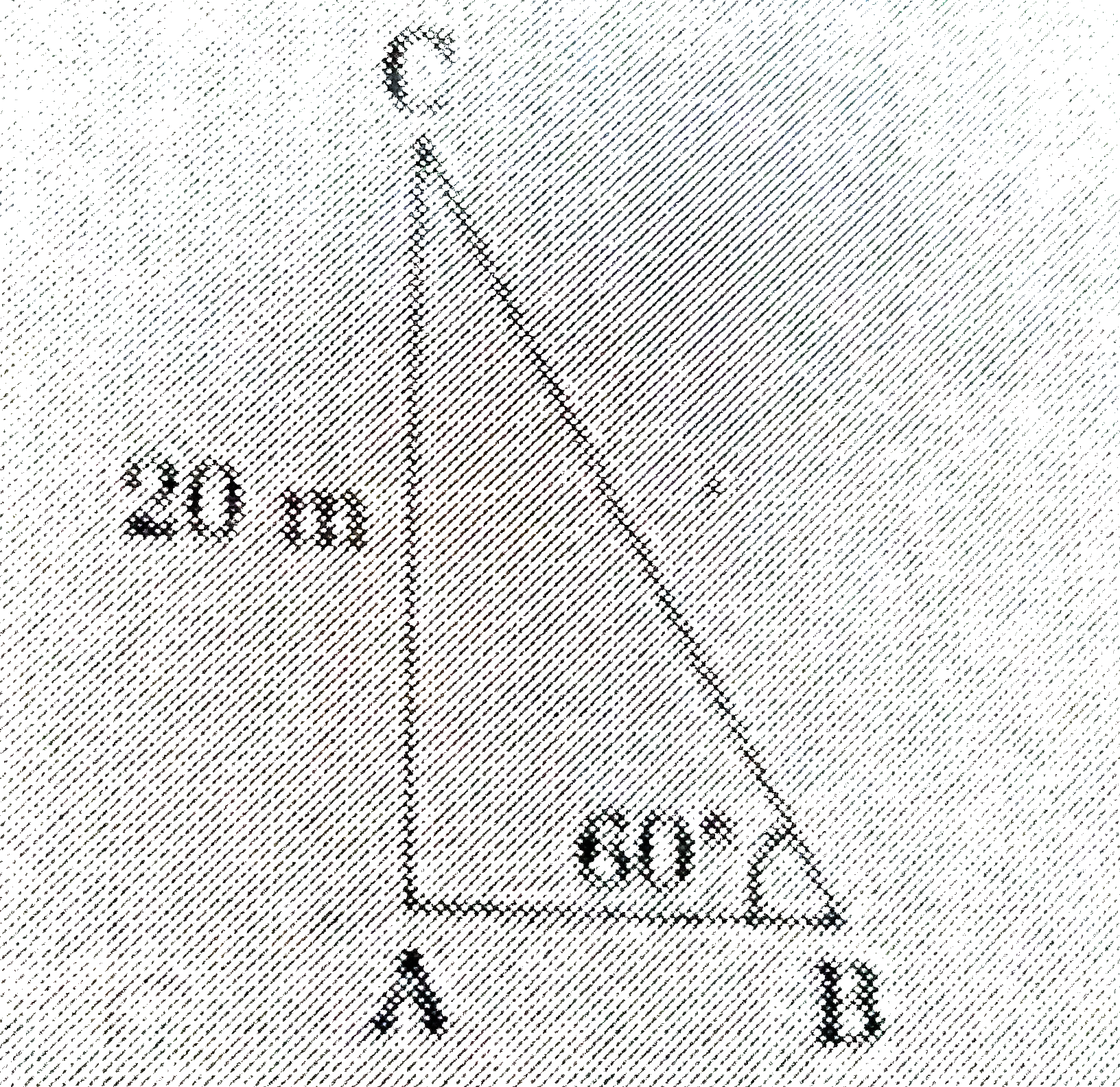
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
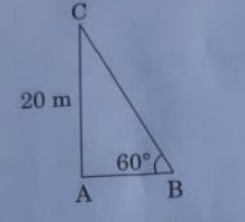
View Solution
