In ΔABC,∠B=90∘ and BD⊥AC.
If CD = 10 cm and BD = 8 cm, find AD.
The correct Answer is:6.4cm
To solve the problem, we will follow these steps:
Step 1: Understand the Triangle Configuration
We have triangle ABC where angle B is 90 degrees. BD is perpendicular to AC, creating two right triangles: ABD and BDC.
Step 2: Label the Known Values
- CD = 10 cm
- BD = 8 cm
- Let AD = x cm (this is what we need to find)
Step 3: Use the Properties of Right Triangles
In triangle ABD, we can express the tangent of angle θ (where θ is the angle at point A) as:
tan(θ)=oppositeadjacent=ADBD=x8
(Equation 1)
In triangle BDC, we can express the tangent of angle θ as:
tan(θ)=oppositeadjacent=BDCD=810
(Equation 2)
Step 4: Set the Two Equations Equal
Since both expressions equal tan(θ), we can set them equal to each other:
x8=810
Step 5: Solve for x
Cross-multiply to solve for x:
10x=8×8
10x=64
x=6410
x=6.4 cm
Step 6: Conclusion
Thus, the length of AD is 6.4 cm.
---
We have triangle ABC where angle B is 90 degrees. BD is perpendicular to AC, creating two right triangles: ABD and BDC.
- CD = 10 cm
- BD = 8 cm
- Let AD = x cm (this is what we need to find)
In triangle ABD, we can express the tangent of angle θ (where θ is the angle at point A) as:
tan(θ)=oppositeadjacent=ADBD=x8
(Equation 1)
tan(θ)=oppositeadjacent=BDCD=810
(Equation 2)
Since both expressions equal tan(θ), we can set them equal to each other:
x8=810
Cross-multiply to solve for x:
10x=8×8
10x=64
x=6410
x=6.4 cm
Thus, the length of AD is 6.4 cm.
Topper's Solved these Questions
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)Book:ICSEChapter:SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)Exercise:EXERCISE 15(B)
Explore 17 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)Book:ICSEChapter:SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)Exercise:EXERCISE 15(C)
Explore 24 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)Book:ICSEChapter:SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)Exercise:EXERCISE 15(E)
Explore 61 Videos
- SIMILARITY Book:ICSEChapter:SIMILARITY Exercise:MULTIPLE CHOICE QUESTIONS (COMPETENCY BASED QUESTIONS)
Explore 10 Videos
- SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)Book:ICSEChapter:SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)Exercise:Exercise 6(e )
Explore 18 Videos
Similar Questions
In ΔABC,∠B=90∘ and BD⊥AC.
If AC = 18 cm and AD = 6 cm, find BD.
View SolutionIn ΔABC,∠B=90∘ and BD⊥AC.
If AC = 9 cm and AB = 7 cm, find AD.
View SolutionIn the given figure, ABC is a right angled triangle with ∠BAC=90∘.

If BD = 18 cm and CD = 8 cm, find AD.
View SolutionIn ΔABC,∠ABC=∠DAC,AB=8cm,AC=4cmandAD=5cm.

Find BC and CD.
View SolutionIn ΔABC,∠B=90∘,AB=12cmandAC=15cm. D and E are points on AB and AC respectively such that ∠AED=90∘ and DE = 3 cm. Calculate the area of ΔABC and then the area of ΔADE.
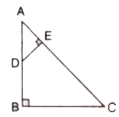
View SolutionIn triangle ABC, AB = AC = 15 cm and BC = 18 cm. Find :
cos B
View SolutionIn given figure, ABC is a triangle right angled at B and BD⊥AC. If AD=4 cm and CD= 5 cm, then find BD and AB.
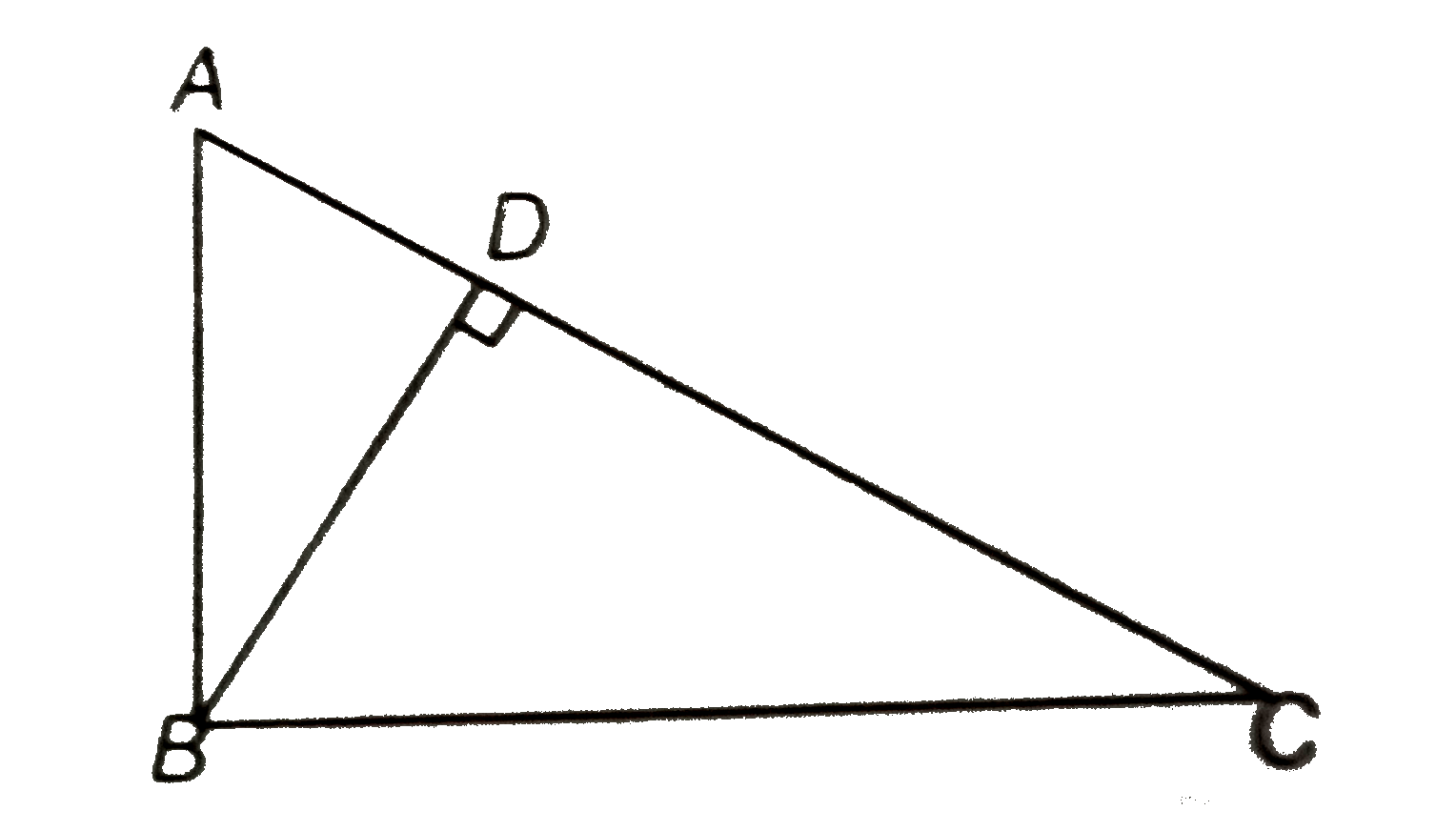
View SolutionIn the following figure ABC is a right angled triangle with ∠BAC=90∘,andAD⊥BC.
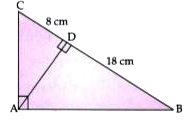
If BD = 18 cm, CD = 8 cm find AD.
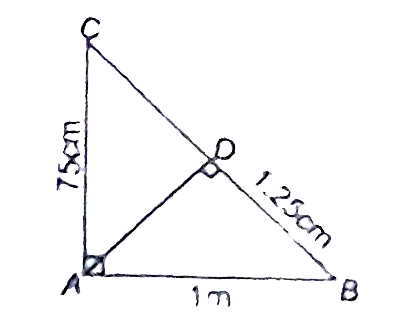
View Solutionin the given figure ∠CAB=90∘andAD⊥BC. if AC= 75 cm , AB= 1m and BD= 1.25 m . Find AD.
View SolutionIn triangle ABC, ∠B=90∘ and tan A = 0.75 If AC = 30 cm, find the lengths of AB and BC.
View Solution

