The point P (5,-4) divides the line segment AB, as shown in the figure, P (5, 4) in the ratio 2:5. Find the co-ordinates of points A and B. Given AP is smaller than BP.
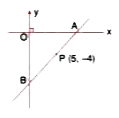
Step by step video & image solution for The point P (5,-4) divides the line segment AB, as shown in the figure, P (5, 4) in the ratio 2:5. Find the co-ordinates of points A and B. Given AP is smaller than BP. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - SECTION AND MID-POINT FORMULAEXERCISE - EXERCISE 13 (B)20videos
SECTION AND MID-POINT FORMULA
- BOOK - ICSECHAPTER - SECTION AND MID-POINT FORMULAEXERCISE - EXERCISE 13 (C)28videos
SECTION AND MID-POINT FORMULA
- BOOK - ICSECHAPTER - SAMPLE PAPER 5 (MATHEMATICS)EXERCISE - SECTION C8videos
SAMPLE PAPER 5 (MATHEMATICS)
- BOOK - ICSECHAPTER - SHARES AND DIVIDENDSEXERCISE - Exercise 3(C )20videos
SHARES AND DIVIDENDS
Similar Questions
P (-3, 2) is the mid point of line segment AB as shown in the given figure. Find the P (-3,2) co-ordinates of points A and B.
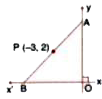 View Solution
View SolutionIf the point P (−1,2) divides the line segment joining A (2,5) and B in the ratio 3:4 , find the co-ordinate of B .
View SolutionThe mid - point of line segment AB (shown in the diagram) is (-3, 5), Find the co-ordinates of A and B.
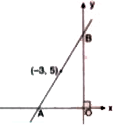 . View Solution
. View SolutionPoint P divides the line segment joining the points A (8,0) and B (16, -8) in the ratio 3:5. Find its co-ordinates of point P.
Also, find the equation of the line through P and parallel to 3x+5y=7.View SolutionIn the given figure, P (4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
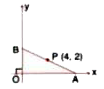 View Solution
View SolutionA line AB meets X-axis at A and Y-axis at B. P(4,−1) divides AB in the ratio 1:2.

Find the co-ordinates of A and B.View SolutionIf a point A lies on the line segment joining the points P(6,0)andQ(0,8) such that AP:AQ=2:3, find the co-ordinates of point A.
View SolutionIf the point C(−1,2) divides internally the line segment joining A(2,5) and B in ratio 3:4, find the coordinates of B.
View SolutionFind the point which divides the line segment joining
(4,5), (-3,4) in the ratio -6 : 5View SolutionPoints A, B, C and D divide the line segment joining the point (5, -10) and the origin in five equal parts. Find the co ordinates of B and D.
View Solution
