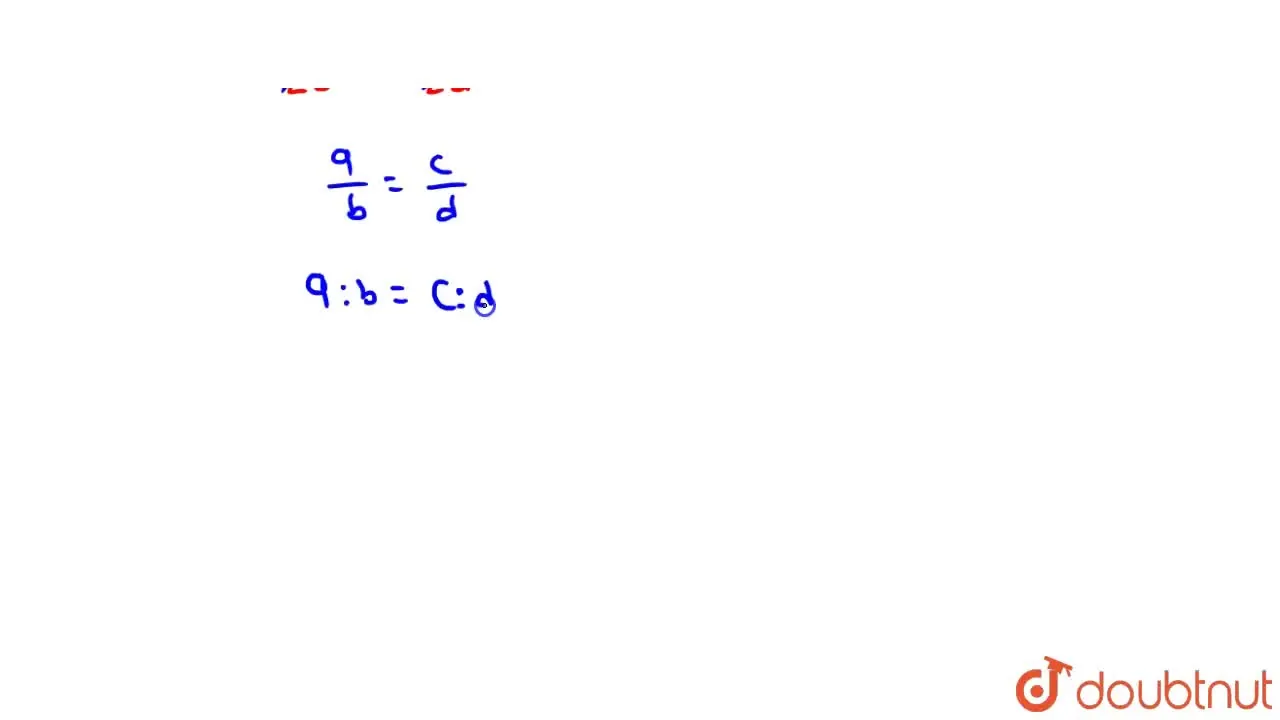If (a+b+c+d)(a−b−c+d)=(a+b−c−d)(a−b+c−d),
prove that: a:b=c:d.
Step by step video & image solution for If (a + b + c + d) (a - b - c + d) = (a + b - c - d) (a - b + c - d), prove that: a : b = c : d. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Related Playlists
- BOOK - ICSECHAPTER - RATIO AND PROPORTION (INCLUDING PROPERTIES AND USES)EXERCISE - Exercise 7(D)27videos
RATIO AND PROPORTION (INCLUDING PROPERTIES AND USES)
- BOOK - ICSECHAPTER - RATIO AND PROPORTION (INCLUDING PROPERTIES AND USES)EXERCISE - QUESTIONS30videos
RATIO AND PROPORTION (INCLUDING PROPERTIES AND USES)
- BOOK - ICSECHAPTER - RATIO AND PROPORTION (INCLUDING PROPERTIES AND USES)EXERCISE - Exercise 7(B)17videos
RATIO AND PROPORTION (INCLUDING PROPERTIES AND USES)
- BOOK - ICSECHAPTER - RATIO AND PROPORTIONEXERCISE - MULTIPLE CHOICE QUESTION61videos
RATIO AND PROPORTION
- BOOK - ICSECHAPTER - REFLECTION EXERCISE - QUESTION1videos
REFLECTION
Similar Questions
If a ,b,c , d are in G.P. prove that
(b + c)(b + d) = (c + a)(c+d)View SolutionIn ABC , if BD⊥AC and BC2=2 ACCD , then prove that AB=AC .
View SolutionIn Fig. 5.10, if AC=BD, then prove that AB=CD.
 View Solution
View SolutionIn Figure, prove that CD+DA+AB+BC>2AC
View SolutionDuring the transformation of .cXa to .dYb the number of β-particles emitted are
a. d+(a−b2)−c b. a−bc
c. d+(a−b2)+c d. 2c−d+a=bView SolutionIn ABC , ray AD bisects ∠A and intersects BC in D . If BC=a , AC=b and AB=c , prove that BD=acb+c (ii) D C = abb+c
View SolutionIn Figure ABDC and ADBC. Prove that ∠DAB= ∠DCB
View SolutionIf a, b, c, d are in proportion, then
(a)ab=cd
(b) ac=bd
(c) ad=bc
(d) None of theseView SolutionIf a,b,c,d are in G.P. prove that: ab−cdb2−c2=a+cb
View SolutionIf a,b,c,d are in G.P., prove that a+b,b+c,c+d are also in G.P.
View Solution