ABCD is an isosceles trapezium with AB parallel to DC, AD = BC = 12 cm, ∠A=60∘andDC=16cm. Taking √3=1.732, find
area of trapezium ABCD.
The correct Answer is:228.62cm2
To find the area of the isosceles trapezium ABCD, we will follow these steps:
Step 1: Understand the given information
We have an isosceles trapezium ABCD where:
- AB is parallel to DC
- AD = BC = 12 cm
- Angle A = 60°
- DC = 16 cm
Step 2: Draw the trapezium
Draw trapezium ABCD with AB parallel to DC. Label the lengths and angles accordingly.
Step 3: Identify the height and bases
Let:
- AB = a (unknown)
- DC = b = 16 cm
- Height = h (unknown)
Step 4: Find the base length (AB)
Since angle A = 60°, we can use trigonometric ratios to find the base length (AB).
In triangle ACD:
- AD = 12 cm (hypotenuse)
- Angle A = 60°
Using cosine to find the base (let's denote the base as x):
cos(60°)=xAD
cos(60°)=x12
Since cos(60°)=12:
12=x12
Multiplying both sides by 12 gives:
x=6 cm
Since AD and BC are equal and symmetrical, the length of the base AB will be:
AB=DC+2x=16+2(6)=28 cm
Step 5: Find the height (h)
Using sine to find the height (h):
sin(60°)=hAD
sin(60°)=h12
Since sin(60°)=√32:
√32=h12
Multiplying both sides by 12 gives:
h=12⋅√32=6√3 cm
Step 6: Calculate the area of trapezium
The area A of a trapezium is given by the formula:
A=12×(a+b)×h
Substituting the values we found:
A=12×(28+16)×(6√3)
A=12×44×6√3
A=22×6√3
A=132√3 cm2
Step 7: Substitute the value of √3
Using √3≈1.732:
A≈132×1.732≈228.624 cm2
Final Answer
The area of trapezium ABCD is approximately 228.624 cm2.
---
We have an isosceles trapezium ABCD where:
- AB is parallel to DC
- AD = BC = 12 cm
- Angle A = 60°
- DC = 16 cm
Draw trapezium ABCD with AB parallel to DC. Label the lengths and angles accordingly.
Let:
- AB = a (unknown)
- DC = b = 16 cm
- Height = h (unknown)
Since angle A = 60°, we can use trigonometric ratios to find the base length (AB).
- AD = 12 cm (hypotenuse)
- Angle A = 60°
cos(60°)=xAD
cos(60°)=x12
Since cos(60°)=12:
12=x12
Multiplying both sides by 12 gives:
x=6 cm
Since AD and BC are equal and symmetrical, the length of the base AB will be:
AB=DC+2x=16+2(6)=28 cm
Using sine to find the height (h):
sin(60°)=hAD
sin(60°)=h12
Since sin(60°)=√32:
√32=h12
Multiplying both sides by 12 gives:
h=12⋅√32=6√3 cm
The area A of a trapezium is given by the formula:
A=12×(a+b)×h
Substituting the values we found:
A=12×(28+16)×(6√3)
A=12×44×6√3
A=22×6√3
A=132√3 cm2
Using √3≈1.732:
A≈132×1.732≈228.624 cm2
The area of trapezium ABCD is approximately 228.624 cm2.
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:CO-ORDINATE GEOMETRY
Explore 6 Videos
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:GRAPHICAL SOLUTION
Explore 3 Videos
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:SOLIDS
Explore 6 Videos
- CHAPTERWISE REVISION (STAGE 1) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 1) Exercise:Graphical solution
Explore 10 Videos
- CIRCLEBook:ICSEChapter:CIRCLEExercise:EXERCISE 17(D)
Explore 12 Videos
Similar Questions
Knowledge Check
ABCD is a trapezium with AB parallel to DC. Then the triangle similar to ΔAOB is:
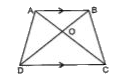 AΔADBBΔACBCΔCODDΔCOB
AΔADBBΔACBCΔCODDΔCOB
In trapezium ABCD, as shown, AB // DC, AD = DC = BC = 20 cm and ∠A=60∘. Find:
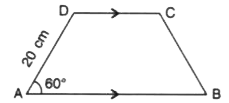
(i) length of AB
View SolutionFind the area of the trapezium ABCD in which AB//DC, AB = 18 cm, ∠B=∠C=90∘, CD = 12 cm and AD = 10 cm.
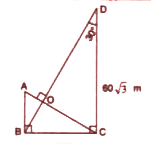
View SolutionIn the given figure, AB⊥BC,DC⊥BC,BD⊥AC,∠D=30∘andDC=60√3 m. Find the length of AB.
View SolutionCalculate the area of the quadrilateral ABCD in which
AB =BD =AD = 10 cm , ∠BCD=90∘andCD=8 cm . (Take √3=1.732).

View SolutionLet ABCD be a trapezium ,in which AB is parallel to CD, AB =11 ,BC=4,CD=6 and DA=3. the distance between AB and CD is
View SolutionIn trapezium ABCD, as shown, AB // DC, AD = DC = BC = 20 cm and ∠A=60∘. Find:
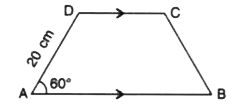
(ii) distance between AB and DC.
View SolutionIn the given figure, ABCD is a trapezium with angle C=120∘,DC=28 cm and BC=40 cm. Find :
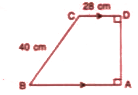
(iii) the area of the trapezium.
View Solution

