The sides of right-angled triangle containing the right angle are 5x cm and (3x- 1) cm. Calculate the lengths of the hypotenuse of the triangle. If its area is 60 cm2
The correct Answer is:17 cm
To solve the problem step by step, we will follow the given information and apply the necessary mathematical concepts.
Step 1: Understand the problem
We have a right-angled triangle with two sides containing the right angle given as 5x cm and (3x−1) cm. The area of the triangle is given as 60cm2.
Step 2: Use the area formula
The area A of a triangle can be calculated using the formula:
A=12×base×height
Here, we can take 5x as the base and (3x−1) as the height. Therefore, we set up the equation:
60=12×5x×(3x−1)
Step 3: Simplify the equation
Multiply both sides by 2 to eliminate the fraction:
120=5x×(3x−1)
Now, distribute 5x:
120=15x2−5x
Step 4: Rearrange the equation
Rearranging gives us:
15x2−5x−120=0
Step 5: Simplify the equation
Divide the entire equation by 5 to simplify:
3x2−x−24=0
Step 6: Factor the quadratic equation
To factor the quadratic equation, we look for two numbers that multiply to −72 (which is 3×−24) and add to −1. The numbers −9 and 8 work:
3x2−9x+8x−24=0
Group the terms:
3x(x−3)+8(x−3)=0
Factoring out (x−3):
(3x+8)(x−3)=0
Step 7: Solve for x
Setting each factor to zero gives:
1. 3x+8=0⇒x=−83 (not valid since x must be positive)
2. x−3=0⇒x=3
Step 8: Calculate the lengths of the sides
Now substitute x=3 back into the expressions for the sides:
- Side AB=5x=5×3=15cm
- Side BC=3x−1=3×3−1=9−1=8cm
Step 9: Calculate the hypotenuse using Pythagorean theorem
Using the Pythagorean theorem:
h2=AB2+BC2
Substituting the values:
h2=152+82=225+64=289
Taking the square root:
h=√289=17cm
Final Answer
The length of the hypotenuse of the triangle is 17cm.
---
We have a right-angled triangle with two sides containing the right angle given as 5x cm and (3x−1) cm. The area of the triangle is given as 60cm2.
The area A of a triangle can be calculated using the formula:
A=12×base×height
Here, we can take 5x as the base and (3x−1) as the height. Therefore, we set up the equation:
60=12×5x×(3x−1)
Multiply both sides by 2 to eliminate the fraction:
120=5x×(3x−1)
Now, distribute 5x:
120=15x2−5x
Rearranging gives us:
15x2−5x−120=0
Divide the entire equation by 5 to simplify:
3x2−x−24=0
To factor the quadratic equation, we look for two numbers that multiply to −72 (which is 3×−24) and add to −1. The numbers −9 and 8 work:
3x2−9x+8x−24=0
Group the terms:
3x(x−3)+8(x−3)=0
Factoring out (x−3):
(3x+8)(x−3)=0
Setting each factor to zero gives:
1. 3x+8=0⇒x=−83 (not valid since x must be positive)
2. x−3=0⇒x=3
Now substitute x=3 back into the expressions for the sides:
- Side AB=5x=5×3=15cm
- Side BC=3x−1=3×3−1=9−1=8cm
Using the Pythagorean theorem:
h2=AB2+BC2
Substituting the values:
h2=152+82=225+64=289
Taking the square root:
h=√289=17cm
The length of the hypotenuse of the triangle is 17cm.
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:SOLIDS
Explore 6 Videos
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:TRIGONOMETRY
Explore 36 Videos
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:MEAN AND MEDIAN
Explore 4 Videos
- CHAPTERWISE REVISION (STAGE 1) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 1) Exercise:Graphical solution
Explore 10 Videos
- CIRCLEBook:ICSEChapter:CIRCLEExercise:EXERCISE 17(D)
Explore 12 Videos
Similar Questions
The sides of a triangle containing the right angle are 5x cm and (3x−1) cm. If the area of the triangle is 60 cm2, calculate the lengths of the sides of the triangle.
View SolutionThe sides of a right angled triangle containing the right angle are 4x cm and (2x-1) cm. If the area of the triangle is 30cm2 calculate the lengths of its sides.
View Solution
Knowledge Check
If length of hypotenuse of a right-angled triangle exceeds the length of one side by 2cm and exceeds twice the length of other side by 1cm, then the length of hypotenuse of the triangle is:
A17cmB1cmC15cmD22cm
Find the area of a right angled triangle whose sides containing the right angle are of lengths 20.8 m and 14.7 m.
View SolutionAn isosceles right triangle has area 8 cm2. The length of its hypotenuse is
View SolutionFind the ara of a right-angled triangle with hypotenuse 25 cm and altitude 24 cm.
View SolutionIn the right-angled triangle QPR, PM altitude.
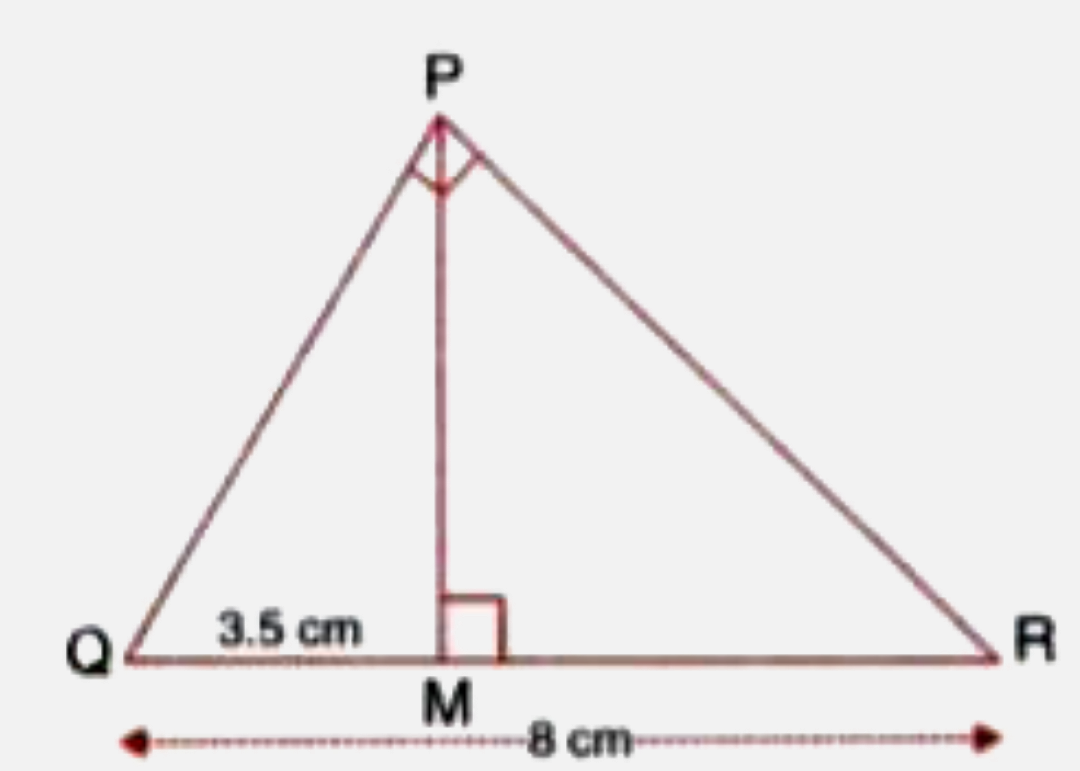
Given that QR = 8 cm and MQ = 3-5 cm, calculate the value of PR.
View SolutionAn isosceles right-angled triangle has area 200 cmWhat is the length of its hypotenuse?
View SolutionIf two sides of a right triangles containing right angle , are equal to corresponding sides of another right angle triangle , the triangle are congruent.
View SolutionThe length of the sides forming right angle of a right angled triangle are 5xcm and (3x−1)cm. If the area of the triangle is 60cm2, find its hypotenuse.
View Solution